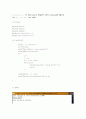
|
풀이를 할 때는 표도 그려야 하고 일일이 계산하는게 귀찮고 번거로웠는데 이렇게 프로그램을 짜서 해보니 구하는 값만 정확히 알면 쉽게 구해짐을 알 수 있었습니다. 이번 과제로 Newton 방법을 더 자세히 알 수 있었던 것 같습니다.
|
|
|
위한 수치해석) Ⅰ. 수치해법이 필요한 이유
Ⅱ. 정확한 해를 구하는 과정
1. 구간법
a. 이분법
b. 선형보간법
2. 개방법
a. 고정점 반복법
b. Newton법
c . Secant법
d . Muller법
Ⅲ. 요 약
Ⅳ. 고 찰
|
|
|
수치해석 방법
2.2.1 Solution of Equation(Secand, False position, Newton)
...............................................................................
2.2.2 Interpolation(Lagrange, Hermite, Spline Interpolation)
..................................................................................
|
|
|
공식 유도
4. 실험결과
①매끈한 원통에서의 결과
②거친 원통에서의 결과
③두 경우의 위치에 따른 속도 분포 그래프
④수치 해석에 의한 각 경우의 항력계수값 계산
(1)C언어를 이용해서 사다리꼴 방법을 이용하여 시도(결국 실패하였습
|
|
|
- - - - - - - - - - - - - - -\");
do{
xi2 = xi - f(xi) / fp(xi);
error = xi2 - xi;
printf(\"\\n %3d %6.4f %6.4f %6.4f %6.4f %6.4f \", count, xi, f(xi), fp(xi), f(xi2), error);
xi = xi2;
count++;
}while(fabs(error)>0.0001 || fabs(f(xi))>0.0001);
printf(\"\\n\\n\\n\\n -- - - - - - - - - - - -
|
|
 |
C. 누가복음의 사회적 배경
2. 누가복음 본문의 위치 및 구조
A. 본문의 위치
B. 본문의 구조: 누가복음 11장
3. 본문의 삶의 자리
4. 본문 분석
5. 본문 대조
6. 중요 단어 분석: “ajnaivdeia”에 따른 비유의 두 가지 해석
1) “밤중에 찾
|
|
|
사용한다면 유아들의 관찰 활동을 격려하고, 동물에 대한 개념을 확장시켜갈 수 있을 것이다. 이는 유아교육 현장에서 이루어지는 동물 관찰 활동이 일반적으로 별 계획 없이 동물을 소개하고 과학영역에 배치하는 것으로 그친다는 점과 실
|
|
|
10ml/min미만인 여성,심한 간부전
renalmin
효능/효과 : 투석환자, 만성신부전에 의한 질소혈증 환자의 vit B,C보급
용법/용량 : 성인 1일 1회 1정
금기 : Vit B12 결핍성 악성빈혈
FERRUN
효능/효과 : 철 결핍성 빈혈의 예방 및 치료
용법/용량 : 성인
|
|
|
Charles E. Merrill Publishing Co.
Laban, R. (1963), Modern educational dance(2nd ed.). London : MacDonald & Evans.
DeMariar, C. R. (1974), Dimensions of physical education. Saint Louis : The C. V. Mosby Co.
Ian Hacking, 선혜영, 황경식 역, 왜 언어가 철학에서 중요한가?, 서울:서광사, 1989.
|
|
|
C. 발달적 게임과 교육체조를 통합한 유아동작교육활동의 효과 검증 절차
1. 연구 대상
2. 실험 설계
3. 검사 도구
4. 연구 절차
5. 자료처리 및 분석
Ⅴ. 연구결과 및 해석
A. 기본운동능력에 미치는 효과
B. 지각
|
|
 |
수치를 시각화했습니다. 그 결과, Critical 인자인 ‘Biscuit Size’를 도출했으며, 10mm 구간에서 다수의 기포 결함이 발생함을 확인했습니다. 이후, 슬리브 3D 모델을 제작해 Anycasting에 적용하고 열유동해석을 수차례 진행했습니다. 그 결과, 최적의
|
|
 |
언어만 바꾸는 것이 아니라, 사용자의 생활 환경과 정서에 맞춘 스토리와 방식이 필요합니다. 그래서 저는 한 콘텐츠가 여러 문화권에 다르게 번역되기보다는, 처음부터 ‘다양한 해석 가능성’을 담고 기획하는 방식을 선호합니다.
13. 아이
|
|
 |
언어는? (마케팅/PR/분석 직무)
19. SKT의 요금제 개선을 위한 신규 타깃 설정 방안과 마케팅 방안을 제시해보세요. (마케팅/PR/분석 직무)
20. LTE망만 있는 지역에 5g 도입시 고려해야할 점과 효율적인 기존 시설 운영 방향을 제시해주세요. (통신
|
|
 |
c영업 중 어느 부분에 더 관심있는가?
12. LTE망만 있는 지역에 5G 도입시 고려해야할 점은 뭘까요?
13. 본인은 공부를 많이 한 사람 같은데 계약직으로 지원한 이유가 뭔가요?
14. ECS, ECR, EKS, Fargate의 차이점은?
15. EC2나 Lambda를 VPC에서 프라이빗
|
|
 |
c사업과 b2b사업의 차이는 무엇이라고 생각하나요? (B2B영업/기술영업 직무)
25. 28Ghz의 특징과 관련 안테나를 설명해보세요 (통신기술/네트워크 직무)
26. 서브넷마스크와 IP고갈 문제에 대해 설명해보세요 (통신기술/네트워크 직무)
27. TCP/IP가
|
|
메뉴펼치기
