|
Fixed-point iteration method
function y = han6(x);
y = 0;
y = x.^2 - 0.2333.*x - 1.8391221 + x;
end
>>fixed_pt_sys(\'han6\', 0, 0.001, 50)
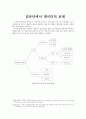
그래프에서 오차의 폭이 커졌다가 작아지는 것을 반복하고 있다. 이는 Fixed-point iteration method의 특징이다. 그렇게 오차의 폭이 변하
|
|
|
Fixed Point Method와 Bisection Method이며 목표는 floating point를 사용하지 않고 Fixed Point Method를 이용하여 Integer형으로 근의 오차를 최대한 줄이며 프로그램 속도를 높이는 것이다.
이 방법들에 대해 간단히 언급한다면 다음과 같다.
Fixed Po
|
|
|
1. 실험목적
● TR의 β를 측정하는 방법을 익히고 Datasheet와 실제값 비교하기
● 세 가지 configuration(Fixed-bias, Emitter-bias, Voltage divider bias)별로, 동작점(Q-point, Dc Bias)이 TR의 β의 변화에 대해 얼마나 영향을 받는지(민감도/둔감도)를 살펴보
|
|
|
fixed point iteration method)
1) 고정점 반복법
f(x)=0을 g(x)=x로 변환 → g(x)를 구하여 의 근사해를 구하는 방법
f(x)=0의 해는 g(x)의 고정점으로서 y=g(x)와 y=x의 두 그래프의 교점의 x좌표
고정함수 g(x)는 여러 가지가 있을 수 있음
초기치 xo와 g(x)의 식의
|
|
|
Fixed point)
1.2 부동 소수점 표현(Floating point)
1.3 10진 데이터
1.3.1 팩 십진수 형식
1.3.2 언팩 십진수 형식
2. 문자 데이터의 표현
2.1 이진 코드
2.1.1 BCD 코드(2진화 10진수)
2.1.2 Gray 코드
2.1.3 3-초과 코드
2.2. 알파뉴메릭 코드(alphanumeric code)
2.
|
|
메뉴펼치기
