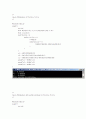
|
Elimination with complete pivoting for Exercise 6.3.4.a
*/
#include<stdio.h>
main(){
int i,j,k;
float M[3][4]={{1,-5,1,7},{10,0,20,6},{5,0,-1,4}};
float t,x1,x2,x3;
for(i=0;i<2;i++){
for(j=i+1;j<3;j++){
if(M[i][0]<M[j][0]){
for(k=0;k<4;k++){
t = M[i][k];
M[i][k] = M[j][k];
M[j][k]
|
|
|
axation)이라고 한다.
식
을 이용하여 새로운 x값을 계산한 후, 그 값을 현재와 직전에 계산된 결과의 가중 평균으로 다음과 같이 놓는다.
여기서 는 가중인자로 0과 2 사이의 값을 갖는데 이 문제에서는 를 1.2로 놓는다.
3번 문제를 partial pivoting
|
|
|
Elimination )
이 방법은 불필요한 변수를 제거시켜 나가는 방법으로 후진소거법의 초기 모형은 완전모형(Full Model)이다. 즉, 첫 단계에는 모든 후보변수를 포함하는 회구모형을 jwr합한 뒤 기여도가 가장 작은(부분 F 통계량의 값이 가장 작은) 벼
|
|
|
pivoting)
근을 구하기 위한 후진 대입 과정에서 대각요소로 나누는 작업이 필요하다. 이때 만약 대각 요소의 값이 '0'이라면 계산이 불가능하게 되고 또한 '0'에 가까운 값이라면 그 계산 결과는 부정확하게 된다.
- 대각요소란
정사각행렬에서
|
|
메뉴펼치기
