|
y1[i]
fprintf(ofp2,"%lf\n",h2_2[i]); //y2출력시 y2[i]
fprintf(ofp3,"%lf\n",h3_3[i]); //y3출력시 y3[i]
}
for(i=0;i<81;i++) //y4출력시 N으로 바꿔줌
{
fprintf(ofp,"%lf\n",h4_4[i]); //y4출력시 y4[i]
}
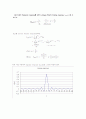
} 1. discrete lowpass filter
2. discrete bandpass filter
3. discrete highpass filter
|
|
|
Filter의 출력 은 다음과 같다.
6) 위의 식을 DTFT(Discrete Time Fourier Transform)할 경우, 다음과 같다.
7) 위의 식에서 , Frequency Response는 Impulse Response를 DTFT한 것이다. 의 크기와 위상을 이용하면 Filter의 각주파수에 대한 특성을 쉽게 파악할 수 있다.
8) L
|
|
|
필터는 기존에 사용되는 통신방식에서 발생되는 전자파 신호의 영향을 많이 받게 되는데 이러한 신호들이 간섭신호로 작용하게 된다. 이러한 환경에서 간섭신호를 제거하기 위해 필터를 사용하게 된다.
Filter란 입력된 여러 주파수 성분 중
|
|
|
void CTestDoc::Lowpass3()
{
int x, y, p, q, div;
int sum, filter1[3][3]={{1,2,1},{2,4,2},{1,2,1}};
div = 0;
for(q = 0;q <=2;q++)
{
for(p =0;p <= 2;p++) div = div + filter1[q][p];
}
for(y = 1;y <255;y++)
{
for(x =1;x < 255;x++)
{
sum = 0;
for(q = 0;q <=2
|
|
|
버릴 수 있게 된다. L과 C를 하나씩 이용하여 구현 가능한 최소한의 2차 필터 기본형은 아래와 같다.
결국 모든 필터의 근본 원리는 이러한 L, C 성분의 조합이라고 할 수 있다. 따라서 Low Pass filter는 이러한 원리에 의해 만들어진다.
캐패시터 C
|
|
 |
필터 설계가 최우선적으로 진행되어야 하며 성능 좋은 Reference 주파수를 사용하여야 한다. VCO의 성능을 개선하기 위해서는 출력단에 Lowpass 필터를 달아줌으로서 하모닉 성분을 제거할 수 있을 것이다. 성능보다는 최종 출력을 얻고자 하였기
|
|
|
를 구한 논문을 찾을 수 있었다.[5] 이 참고문헌을 이용해 초기 설정 값을 근사 값으로 정하여 ADS tool을 이용한다면 보다 빠르게 제작을 할 수 있을 것으로 생각된다.
참고 문헌
[1] Kamaljeet Singh, R. Ramasubramanian, S. Pal, “Coupled Microstrip Filters: Simple
|
|
|
Filter", IEEE Proceeding Electirc Power Application, vol. 141, no. 3, 1994.
〔7〕한병문, 김희중, 박덕희, 소용철, "단상 능동전력필터의 새로운 제어방식", 대한전기학회 추계학술대회 논문집, 1998
(Abstract)
Single-Phase Active Power Filter
with One Current Sensor
Sung-ryong, Kim
|
|
|
필터에서는 앞에서 구현하였던 인덕터를 사용한 low pass filter 형태의 회로를 추가하여 일정한 주파수 이하에서는 전압의 공급을 차단시키는 역할을 함으로써 VCDL에 인가되는 전압의 양을 조절하게 된다. <8>
원래 1차 시스템인 DLL에서는 단
|
|
|
Filter 설계
Ⅳ-1. Low Pass Filter
Ⅳ-2. LPF Code
Ⅳ-3. Band Pass Filter
Ⅳ-4. BPF Code
V. DSB-SC의 시스템 설계
Ⅴ-1. DSB-SC Modulation
Ⅴ-2. DSB-SC Demodulation
Ⅴ-3. Carrier 선정
Ⅵ. 결과 및 분석
Ⅵ-1. 구현 Code
Ⅵ-2. 송신단 결과
Ⅵ-3. 수신단 결과
Ⅵ-4
|
|
 |
Filter .
환율 증가 지속 로밍 수요 증가 및 전송속도 향상을 위한 이중연결 및 , E-UTRA NR (EN-DC) 4X4
MIMO 지원이 필수인 스마트폰 수요 증가로 기기 당 탑재되는 고 성능 필터의 개수는 폭발적 증가
세를 나타내고 있습니다 1. 기업분석
1.1
|
|
 |
UNCH LIST 작성,
보완.
4) 사업장 내 Scrubber, Cyclone, Bag-Filter 설비 연간 유지 보수 및 관리
- 대기오염물질 배출시설 유지 상태 확인.
- 대기 배출원 관리시스템(SEMS)입력 및 반기자료 구청 제출업무 수행.
- 대기환경보전법 개정자료(사업장 해당 분)
|
|
 |
1 Piezo Device에 대해 설명해 주세요
2 반도체 8대공정 설명 그리고 먼 지역에서 어떤계기로 경기도까지 올라왔는지
3 Saw filter란? 대학시절부터 해온 활동중 반도체 관련 경험?
4 외국어 테스트:자기소개 및 장단점 영어로 말해주라
5 rf 지식에
|
|
 |
① 1차 실무진 면접 / 공정
1 Piezo Device에 대해 설명해 주세요
2 반도체 8대공정 설명 그리고 먼 지역에서 어떤계기로 경기도까지 올라왔는지
3 Saw filter란? 대학시절부터 해온 활동중 반도체 관련 경험?
4 외국어 테스트:자기소개 및 장단점
|
|
 |
Filter 등의 다양한 전자통신 분야의 프로젝트와 캡스톤 설계를 경험 하였고, 학과 실험에서도 좋은 결과를 보여 왔습니다.
(중 략)
대학에서 배운 이론과 적성, 창조와 도전 열정을 합하여 최고의 능력을 발휘할 수 있을 것이라 생각합니다.
|
|
메뉴펼치기
