스포츠경제학 ) LG twinz와 kt wiz의 두팀모델 분석

소개글

스포츠경제학 ) LG twinz와 kt wiz의 두팀모델 분석에 대한 보고서 자료입니다.

목차

1. 서울과 수원의 시장 크기 및 구매력의 차이를 나타낼 수 있는 데이터를 찾아서 제시
2. 위의 데이터를 토대로 두 팀의 장기이윤최대화모델 수익 곡선
3. 수익 곡선을 토대로 한계수익 곡선을 그리고 두 팀의 수익 곡선과 한계수익 곡선이 차이점에 대해 논의
4. 두 팀의 한계수익 곡선을 토대로 두 팀 모델을 이용해 분석한 뒤 균형점에서의 LG와 kt의 승률 차이에 대해 논의하고, 실제 데이터와 비교
5. 균형점에서 두 팀의 총 연봉지출액을 그래프상에 나타내고 어느 팀이 더 많은 지출을 하고 있는지 논의한다. 또한 실제 데이터와 비교한다.
6. 현재까지 분석한 가상의 KBO 두 팀 리그에 FA 연봉 상한제가 도입되었다. 이 FA 연봉 상한제는 두 팀의 실력 차를 줄여서 리그의 결과가 두 팀이 균등하게 50%의 승률 가져갈 수 있도록 정해졌다고 한다. 이 연봉 상한제로 인해 나타나는 새로운 균형점과 그에 따른 결과를 두 팀 모델을 이용해서 분석하고 논의한다. (새로운 균형점에서 두 팀의 승률, 총 연봉지출액, 그리고 리그 전체의 총 연봉지출액을 연봉 상한제 이전과 이후의 차이로 분석한다.)

본문내용

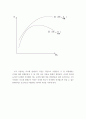
있다. 마켓잠재력 A(서울)> B(수원).
2. 위의 데이터를 토대로 두 팀의 장기이윤최대화모델 수익 곡선
서울의 마켓 잠재력 A(서울)가 수원의 마켓 잠재력 A(수원)보다 더 크다.
3. 수익 곡선을 토대로 한계수익 곡선을 그리고 두 팀의 수익 곡선과 한계수익 곡선이 차이점에 대해 논의
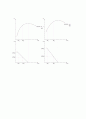
수익 곡선과는 다르게 한계수익 곡선은 직선으로 가정한다. 두 팀 모델에서는 승리를 위한 한계비용이 두 팀 간의 상호 작용을 통해서 결정된다. 승리의 횟수를 늘려가기 위해서 투자해야 하는 승리에 대한 비용 한계지출은 점차 증가하므로 수익 곡선과는 다르게 한계수익 곡선은 승리의 횟수가 증가하면 증가할수록 얻을 수 있는 한계이익은 감소하므로 체감하는 형식의 곡선을 가지게 된다.
4. 두 팀의 한계수익 곡선을 토대로 두 팀 모델을 이용해 분석한 뒤 균형점에서의 LG와 kt의 승률 차이에 대해 논의하고, 실제 데이터와 비교
두 팀의 한계수익 곡선을 하나로 합친 그래프이다. 균형점에서의 승률은 각각 W(수원), W(서울)로 나누어지는데, 서울에서의 마켓 잠재력이 더 높으므로 서울의 승률이 더 높아야 한다.
그런데 실제 2020년도 KBO 시리즈 KT위즈의 승률은 0.566이고 LG twins의 승률은 0.564이다. 이러한 결과는 예상했던 결과와는 다른 결과를 보여준다. 실제로 승리에 영향을 미치는 변수는 위의 모델에서 승리 확률에 영향을 미칠 것으로 생각했던 변수들보다도 많은 것에 영향을 받기 마련이다. 실제 리그는 두 팀 리그가 아니라 여러 팀이 참가하는 리그라는 점에서도 차이가 난다. 따라서 두 팀 모델의 결과와 실제 리그의 결과는 같을 수 없다.
5. 균형점에서 두 팀의 총 연봉지출액을 그래프상에 나타내고 어느 팀이 더 많은 지출을 하고 있는지 논의한다. 또한 실제 데이터와 비교한다.
군형점에서 서울팀이 더 많은 지출을 하고 있음을 알 수 있다. 승리의 확률을 증가시키기 위해선 한계지출을 늘려야 하고 이에 따라 서울의 총연봉은 수원과 비교하여 상승해야 한다.
실제로 신인 선수와 외국인 선수를 제외한 KT위즈 선수단의 2020년도 평균 연봉은 1억 40만 원이고 마찬가지로 신인 선수와 외국인 선수를 제외한 LG twins의 2020년도 평균 연봉은 1억 6,148만 원이다. 서울에 연고지를 둔 LG twins의 연봉이 약 6,100만원 정도 평균적으로 높은 것이다.
6. 현재까지 분석한 가상의 KBO 두 팀 리그에 FA 연봉 상한제가 도입되었다. 이 FA 연봉 상한제는 두 팀의 실력 차를 줄여서
리그의 결과가 두 팀이 균등하게 50%의 승률 가져갈 수 있도록 정해졌다고 한다. 이 연봉 상한제로 인해 나타나는 새로운 균형점과 그에 따른 결과를 두 팀 모델을 이용해서 분석하고 논의한다.
(새로운 균형점에서 두 팀의 승률, 총 연봉지출액, 그리고 리그 전체의 총 연봉지출액을 연봉 상한제 이전과 이후의 차이로 분석한다.)
리그에서 연봉상한제를 이용하여 승리를 위한 한계비용 p를 변화시켜 두 팀의 승률을 모두 50:50으로 설정하였다. 승리 한계비용 p를 서울팀에는 상승시키고 수원팀에는 하락시켰다. 이에 따라, 승리 한계비용이 높아진 서울 팀은 이전과 비교하여 낮은 성적을 택하였고, 승리 한계비용이 낮아진 수원팀은 조금 더 높은 성적을 택함으로써 새로운 균형점 승률 50%를 맞출 수 있었다. 서울팀의 연봉지출액은 줄어들었으며 수원팀의 연봉지출액은 늘어났다. 리그 전체의 총 연봉지출액은 변함없다.
4. 출처 및 참고문헌
통계청, e-지방지표
https://kosis.kr/statHtml/statHtml.do?orgId=101&tblId=DT_1YL0000&conn_path=I2

키워드

과제,   레포트,   논문,   사이버,   학점은행,   일반대학,   오프라인,   온라인,   일지