현대제어보상기설계

소개글

현대제어보상기설계에 대한 보고서 자료입니다.

목차

step1>

step2>

step3>

step4>

▷문제 해석◁

본문내용

.하지만 그 범위에서는 PM이 40 이상이 되지 않는 다는 것을 확인해 볼수 있었고,
그래서 이번 문제는 2단 보상기라 생각하고 문제를 해결하여야 했다.
처음 해보는 것이라 생소해서 문제를 푸는데 어려움이 있었다.
원하는 PM을 얻기 위해서 단순히 1단 보상기로만 해결해야 한다는 생각을 하고 있었는데, 이번 문제를 해결하면서 문제를 해결하기위해 이런저런 방법을 생각해 보는 좋은 기회가 되었던 것 같다.
%문제에서 주어진 값
n=[25];
d=[1,6,5,0];
H=tf(n,d);
bode(H)
[GM,PM,Wcg,Wcp]=margin(H)
%1단 보상기로 되는지 확인
w=[2.0:0.01:3.5];
[mag,phase]=bode(H,w)
MAGDB = 20*log10(mag)
%2단 보상기라 가정하고 문제 풀이 시작
paimax1=36;
radian=pi/180;
alpha=(1-sin(radian*paimax1))/(1+sin(radian*paimax1))
wg1=10*log(alpha)
w=[2.5:0.01:3.5];
[mag1, phase1]=bode(H, w)
bode(H)
MAGDB1 = 20*log10(mag1)
%새로운 gcf 값을 넣어주고 계산(한번 보상한 전달함수 구함)
wg=3.24;
T=1/(wg*sqrt(alpha))
d1=[alpha*T 1];
n1=[T 1];
den=conv(d, d1);
num=conv(n, n1);
[mag, phase, w]=bode(num, den)
[GM1,PM1,Wcg1,Wcp1] = margin(mag,phase,w)
H=tf(n,d);
H2=tf(num, den);
%두번째 보상한 전달함수 구함(이때 알파값은 같다고 가정하자)
w=[4.0:0.01:4.3];
[mag2, phase2]=bode(H2, w)
MAGDB2 = 20*log10(mag2)
wg2=4.08;
T1=1/(wg2*sqrt(alpha))
d2=[alpha*T1 1];
n2=[T1 1];
den1=conv(den, d2);
num1=conv(num, n2);
[mag7, phase7, w7]=bode(num1, den1)
[GM7,PM7,Wcg7,Wcp7] = margin(mag7,phase7,w7)
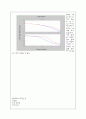
%문제에서의 그래프 H와 보상한 후의 그래프 H3를 한꺼 번에 표현.
hold off;
H=tf(n, d);
H3=tf(num1, den1)
bode(H, 'b', H3, 'r');

키워드

현대제어,   보상기,   LEAD,   설계,   매트랩