이차함수

목차

1. 서론
<연구 방향>

2. 본론
<논의로 들어가기에 앞서>
<기존 학교 함수 개념 지도의 문제점과 그 대책>
< 이차함수로의 컴퓨터를 통한 접근 >

본문내용

록일 수 있는 성질을 바탕으로 해서, 과연 어떤 것을 추론해 낼 수 있는 지 알아보는 과정 중 절대값이 같은 이차 계수를 가진 기본형
y=ax^2
가 어떤 특징을 가지고 있는지를 심화 탐구해 보는
과정을 나타낸 그림이다. 물론 학생들이 쉽게 얻을 수도 있겠지만, 이를 집어내어 다시금 생각해 보게 하는 것이 중요하다. 일단, 버튼으로 절대치가 같은 경우 어떻게 될지를 생각해 보게 하는 것이 교사가 해야 할 일이라 하겠다. 이렇게 함으로써, 학생들은 단지 그림 그리기 차원에서 벗어나, 새로운 논의로의 전개를 손쉽게 할 수 있는 것이다. 클릭 A와 클릭 B를 통해서는 실제 절대값이 같고, 부호만 다른 두 기본형을 자취를 그려봄으로써, 어떤 특징이 있는지를 알아볼 수 있는 것이다. x축에 대칭임, 폭은 일정함을 확인한다면, 그것으로 수업을 이끌어 온 효과를 누릴 수 있는 것이라 하겠다.
(세 번째 수업시간)
세 번째 수업시간에는 지난 시간에 논의한 기본꼴을 토대로 그것에서 조금 더 확장되어진 논의를 전개한다.
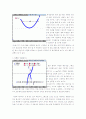
좌측 그림에서 button ss {'식 y=2x²+',10*mc(v_25,v_15);0.5,-0.6}; 를 이용하여 실제 좌측 아래에 있는 식에서 위아래로 움직였을 때의 자취를 쉽게 구할 수 있도록 만들어 놓았다.
학생들은 이것을 토대로 식이 어떻게 변화해 가는 지를 알 수 있는데, a값을 택하지 못하는 게 아쉬움으로 남았다. 물론,
또 하나 위 button식에서와 같이 mc를 통해서는 거리 측정만이 가능하여, y좌표가 음수로 가면 인지하지 못한다는 문제가 있었고, 이에 따라 한번 두 가지 그래프의 형태를 달리 잡아 식으로 만들어 보았다. 학생들에게 제시되려면, 이것을 단순화하여, 조금 혼돈될 수 있을 만한 부분을 미연에 방지하는 것이 가장 좋을 것이다. 학생들에게 스스로 이런 활동을 해보도록 하는 것은 아이들이 처음에 만들어 본 다양한 형태의 이차함수로 접근해 감에 있어서 식을 토대로 전개해 간다는 것을 알도록 한다는 점에서 중요하다. 점차 개념이 확장되어, 꼭지점을 원점으로 하는 기본형에서 y축 위로 움직이는 그래프로, 한단계 더 나아가 x축위로 움직이는 그래프를 그려보는 것이 이차함수 식으로서의 확장일 것이다. 이런 형태를 학생들이 실제 만들어보고, 연속해서 함수 식이 구해짐을 확인하여, 다시 저런 함수식을 접했을 때, 기본적으로 떠올릴 수 있도록 하기 위한 토대로써 작용할 수 있는 것이라 하겠다. 이차함수 식을 바탕으로 해서 삼차함수, 사차함수를 그리기 위해서는 이런 개념적인 접근 하나하나가 중요한 기제로써 작용할 것이라 본다.
* 기본형
y=a(x-p)^2
꼴 모양의 전개식~
이와 같은 것을 전개함에 있어서도 DGS를 통한 학습 방법이 효과적이다.
학생들은 그래프를 컴퓨터를 통해 정확하게 그릴 수 있는데, 이를 통해서 보다 개념을 인식하는 데 있어서 바탕 원리로써 효과적으로 사용되어 질 것이다.
교사들은 앞에서 y축을 따라 이동한 것을 근거로 하여, x축 위로의 접근을 시도한다. 학생들은 교실 수업에서의 일방적인 수업과 다르게 새롭게 시도해 보고, 다양한 함수들로서 조작하는 것을 자신이 마음대로 정할 수 있다는 자율적인 면에 많은 학생들이 적극적으로 참여할 것이라고 본다. 교사는 그 방향을 잘 설정해 주어, 학생들이 귀납적으로 실험을 통해 얻은 지식을 연역적 원리 또는 식을 구성하는 데 효과적으로 사용될 수 있도록 지도하여야 할 것이다. 학생들은 자신들이 자율적으로 학습을 할 수 있는 만큼, 다양한 시도를 할 것인데, 항상 염두해 두어야 할 것들은 바로 이런 낱낱개의 프로그램이 전체적으로 연결 고리를 찾아서 지속적으로 개념을 확장시켜 갈 수 있도록 해야 한다는 것이다. 교사들이 이런 원리를 통해서 학생들 스스로가 새로운 원리를 습득하고, 창의력을 발휘할 수 있도록 도와 주는 역할을 해야만 한다.
왼쪽 그림에서도 자율적인 면이 강조된다. 자취를 좇는 그림이라 조금 깔끔하게 전개되지 않는 면도 있겠지만, 이런 작용을 지속적으로 시도해 감으로써 학생들은 식이 어떻게 구성되어 지며, 그래프로 어떻게 구현되어 지는가를 구체적으로 알 수 있는 것이 장점이라 하겠다. 왼쪽 그림에서도 위의 예제와 같이
버튼 q {'B 식 y=-2(x-',mc(v_8,P)*10;0.4,-1.2;}
을 통해, P에 따라 움직이는 좌표의 연속성을 그래프의 식을 통해 감지할 수 있도록 만들었다. 교사는 이것을 토대로 연속적인 자취의 움직임과 그래프를 통해 학생들이 모눈종이나 종이를 통해서는 획득할 수 없는 것들을 인식할 수 있음을 인지하고, 적극 활용해야 한다. 학생들이 또한, 이런 원리를 토대로 더욱 발전적이고 발산적인 논의를 해 나가는 데 있어, 교사가 적극적으로 연결 끈을 이어 주어야 하겠다.
결론에 들어가서
이차함수는 중3 교과서에서 한 단원을 차지하고 있을 정도로 비중있게 다루어진다. 그러나, 많은 학생들이 교과서 내의 논의를 종이만을 가지고 전개해 가는 데 어려움을 느낀다. 더군다나 요새 아이들처럼 시각화 매체에 잘 적응이 되어 있는 아이들에게 종이에 적혀 있다고 무조건적으로 외우게 한다거나, 시각화를 거치지 않은 상태로 추론만 하도록 하는 것은 옳지 않다. 조금씩 이라도 학생들이 스스로 만들어보고, 조작할 활동을 제시해 주어야 한다. DGS를 통한 접근은 프로그래밍과 다르게 누구나 손쉽게 할 수 있으므로, 학생들도 조금만 원리를 가르쳐 준다면, 학습을 하는 데 있어 많은 고리타분한 이야기들을 줄이고, 활동적으로 재미있게 수학 교실도 만들 수 있는 것이다.
물론, DGS를 통한 논의가 시각적 자원에서만 머무르는 것은 아니며, 이것이 더욱 발전적인 논의 과정 속에서 연역적으로 학생들에게 인지되어 질 수 있는 작용이 교실에서 이루어져야 한다. 학생들에게 있어서 직관적으로 인식될 수 있는 것일지라도, 그것이 왜 그렇게 되는지, 그리고 그것을 통해 알 수 있는 사실은 무엇인지, 스스로 보고 인지한 바를 토대로 하여 전개해 간다면, 단지 교수주의적 차원이 아니라, 스스로 구성하고, 만들어 갈 수 있도록 해 주어야한다는 구성주의의 토대로서도 손색이 없을 것으로 생각된다.

키워드

이차함수,   함수,   이차