공간 데이터 마이닝을 위한 효율적인 그리드 셀 기반 공간 클러스터링 알고리즘

목차

1. 목적

2. 공간 클러스터링 기법

3. 공간 클러스터링 알고리즘

4. 실험 결과

5. 결론 및 향후 연구

본문내용

1. 목적
기존 공간 클러스터링 알고리즘들은 객체들간의 거리를 기반 계산 비용 증대
공간 지역성을 보장하는 대표적인 공간분할 방법인 그리드 셀을 기반  계산 비용 감소
2. 공간 클러스터링 기법
기존 클러스터링의 문제점
그림1
객체들간의 거리 연산에 많은 비용
기준객체와 다른 객체들간에 거리 계산이 필요
다른 클러스터 검색과정에서도 위의 과정이 반복
그리드 셀 기반 클러스터링
이 기법의 핵심
그리드 셀 구조를 기반으로 한 셀 관계 연산을 통하여 클러스터링을 하는 것
기존의 객체들간 거리 계산에 의한 비용을 감소시킴
전체 공간 영역에 대하여 그리드 셀 구조를 생성
사용자가 부여한 임계값()을 기준으로 셀 크기 결정  그림 2
3. 공간 클러스터링 알고리즘
3.1 셀 관련성 정의
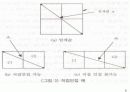
직접 인접
그리드 셀 구조에서 임의의 셀 C1과 C2간의 최대거리가 임계값 보다 작거나 같다 - 그림3
직접 인접 셀(DAC:Direct Adjacent Cells)
기준 셀에 대하여 직접인접 관계에 있는 셀들로 정의(최소3개, 최대 8개)
인접 가능
임의의 셀들 C1,C2,C3에 대하여, C1과C2가 직접인접하고 C2와C3가 직접인접하면 C1과C3는 인접 가능 – 그림4
클러스터링 전파(Clustering propagation)
공간 객체들이 존재하는 임의의 셀들 C1,C2,C3에 대하여 C1과C3가 C2를 기반으로 하여 인접 가능하면, C1과C3 셀간에는 클러스터링이 가능 – 그림5
3.2 클러스터링 생성 알고리즘
셀 기반 공간 클러스터링 알고리즘
클러스터 생성 알고리즘과 클러스터 합병 알고리즘으로 구성
클러스터 생성 알고리즘
직접인접, 직접인접 셀, 인접가능, 클러스터링 전파(반복) 정의를 이용하여 클러스터 생성 –그림7
그림 6, 그림 8
3.3 클러스터링 합병 알고리즘
클러스터링 합병 알고리즘 필요성
클러스터링 생성 알고리즘은 후보 클러스터들을 생성
생성된 클러스터들에 포함된 객체간의 거리를 기준으로 보면 임계값 이내에 존재하는 객체들이 존재
그림8

키워드

공간 데이터 마이닝,   그리드 셀,   클러스터링