본문내용
거의
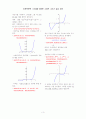
0
에 가깝다. 즉
{ x^{ 3 } } over { x^{ 2 } +1 } ` APPROX x``
,
x` -> INF
그래프를 그리는데 plot를 사용하였다.
plot에는 많은 옵션이 있어 옵션을 적절히 잘 사용하면 원하는 형태의 그래프를 그릴 수 있다. 옵션에 대한 정보는 워크시트에서 다음을 입력하면 된다.
> ?plot
실습문제
A-H의 지침을 따라 다음 곡선을 그려라.
(a)
y=x^{ 3 } +`6`x^{ 2 } +9x
(b)
f(x)=`2`cos`x``+`sin`2`x
(c)
f(x)=` { x^{ 3 } -1 } over { x^{ 3 } +1 }
(d)
f(x)`=` { x^{ 2 } +7x+3 } over { x^{ 2 } }
Maple의 기본 사용법
-명령문의 구분 ; 또는 :
-명령문의 실행은 Enter key
예) 1+1/2; sqrt(2)+Pi; x+2*x;
- lhs:=rhs는 우변의 값을 좌변의 변수 에 할당하는 것이다.
예) f:=x^2+sin(x);
변수를 할당하면 할당 해제 또는 다른 변수값 할당이 없는 한 f는 x^2+sin(x)의 값을 취한다.
-f:=\'f\':로 변수할당을 해제할 수 있다. -%는 직전의 실행결과 값을 이어 받는 연산자이다.
함수값 구하는 방법
함수값을 구하는 방법은 두 가지가 있다. (a) 함수를 정의한 후 값을 대입하는 경우
> f:=x->x^3+2*x-5;
> f(1);
-1
(b) 대입을 이용한 방법
> subs(x=1,x^3+2*x-5);
-1
(b)의 방법은 변수할당이 불필요한 곳에
사용하면 좋다.
0
에 가깝다. 즉
{ x^{ 3 } } over { x^{ 2 } +1 } ` APPROX x``
,
x` -> INF
그래프를 그리는데 plot를 사용하였다.
plot에는 많은 옵션이 있어 옵션을 적절히 잘 사용하면 원하는 형태의 그래프를 그릴 수 있다. 옵션에 대한 정보는 워크시트에서 다음을 입력하면 된다.
> ?plot
실습문제
A-H의 지침을 따라 다음 곡선을 그려라.
(a)
y=x^{ 3 } +`6`x^{ 2 } +9x
(b)
f(x)=`2`cos`x``+`sin`2`x
(c)
f(x)=` { x^{ 3 } -1 } over { x^{ 3 } +1 }
(d)
f(x)`=` { x^{ 2 } +7x+3 } over { x^{ 2 } }
Maple의 기본 사용법
-명령문의 구분 ; 또는 :
-명령문의 실행은 Enter key
예) 1+1/2; sqrt(2)+Pi; x+2*x;
- lhs:=rhs는 우변의 값을 좌변의 변수 에 할당하는 것이다.
예) f:=x^2+sin(x);
변수를 할당하면 할당 해제 또는 다른 변수값 할당이 없는 한 f는 x^2+sin(x)의 값을 취한다.
-f:=\'f\':로 변수할당을 해제할 수 있다. -%는 직전의 실행결과 값을 이어 받는 연산자이다.
함수값 구하는 방법
함수값을 구하는 방법은 두 가지가 있다. (a) 함수를 정의한 후 값을 대입하는 경우
> f:=x->x^3+2*x-5;
> f(1);
-1
(b) 대입을 이용한 방법
> subs(x=1,x^3+2*x-5);
-1
(b)의 방법은 변수할당이 불필요한 곳에
사용하면 좋다.
추천자료
 변수와 척도
변수와 척도 범죄자처우 이념의 변모와 새로운 사회내처우 프로그램의 변화
범죄자처우 이념의 변모와 새로운 사회내처우 프로그램의 변화 오실로스코프를 이용한 측정(리사쥬 패턴)
오실로스코프를 이용한 측정(리사쥬 패턴) 이라크에 전쟁이 났을 때, 석유시장에 미치는 영향과 LPG시장에 미치는 영향/자기주변에서 ...
이라크에 전쟁이 났을 때, 석유시장에 미치는 영향과 LPG시장에 미치는 영향/자기주변에서 ... 통계교육(통계지도) 개념, 통계교육(통계지도) 목표와 필요성, 통계교육(통계지도) 경향과 과...
통계교육(통계지도) 개념, 통계교육(통계지도) 목표와 필요성, 통계교육(통계지도) 경향과 과... [조사학습][조사학습 의의][조사학습 유형][조사학습 절차][조사학습 유형별 사례][조사학습 ...
[조사학습][조사학습 의의][조사학습 유형][조사학습 절차][조사학습 유형별 사례][조사학습 ... 제출용지도안
제출용지도안 [초등학교 6학년 확률과 통계 수업지도안]
[초등학교 6학년 확률과 통계 수업지도안] [마케팅조사론] 꼬꼬면 소비자 조사 보고.PPT자료
[마케팅조사론] 꼬꼬면 소비자 조사 보고.PPT자료 MATLAB05
MATLAB05 [조사, 조사 필요성, 조사 과정, 조사 조사원 역량, 조사 결과생산, 조사 고려사항]조사의 필...
[조사, 조사 필요성, 조사 과정, 조사 조사원 역량, 조사 결과생산, 조사 고려사항]조사의 필... 모성 가족계획과 피임 - 가족계획과 피임법.ppt
모성 가족계획과 피임 - 가족계획과 피임법.ppt 꼬꼬면 시장점유율 증대및 재포지셔닝위한 마케팅조사 분석 (면접,설문조사 자료포함)
꼬꼬면 시장점유율 증대및 재포지셔닝위한 마케팅조사 분석 (면접,설문조사 자료포함)

























소개글