목차
Ⅰ. Group Technology의 이론
1. GT의 정의와 발전과정
(1) GT의 정의
(2) GT의 발전과정
2. GT의 활용부문 및 효과
(1) GT의 활용 - 설계, 기술부문
(2) GT의 활용 - 생산부문
(3) GT의 활용 - 기타 경영부문
(4) GT의 효과
(5) GT의 적용사례
Ⅱ. Group Technology Problem
1. Following algorithms :
ⅰ. Single linkage cluster algorithm (SLCA)
ⅱ. Rank order algorithm (ROC)
ⅲ. Direct cluster algorithm (DCA)
ⅳ. Bond energy algorithm (BEA)
2. Define and find the bottleneck elements, and suggest the way how to handle with those elements.
(ⅰ) Duplication (기계 추가)
(ⅱ) Elimination (공정 제거)
(ⅲ) Subcontract (하청업체)
(ⅳ) Assignment (할당)
3. Find out the grouping efficiency of each case.
ⅰ. Single linkage cluster algorithm (SLCA)
ⅱ. Rank order algorithm (ROC)
ⅲ. Direct cluster algorithm (DCA)
1. GT의 정의와 발전과정
(1) GT의 정의
(2) GT의 발전과정
2. GT의 활용부문 및 효과
(1) GT의 활용 - 설계, 기술부문
(2) GT의 활용 - 생산부문
(3) GT의 활용 - 기타 경영부문
(4) GT의 효과
(5) GT의 적용사례
Ⅱ. Group Technology Problem
1. Following algorithms :
ⅰ. Single linkage cluster algorithm (SLCA)
ⅱ. Rank order algorithm (ROC)
ⅲ. Direct cluster algorithm (DCA)
ⅳ. Bond energy algorithm (BEA)
2. Define and find the bottleneck elements, and suggest the way how to handle with those elements.
(ⅰ) Duplication (기계 추가)
(ⅱ) Elimination (공정 제거)
(ⅲ) Subcontract (하청업체)
(ⅳ) Assignment (할당)
3. Find out the grouping efficiency of each case.
ⅰ. Single linkage cluster algorithm (SLCA)
ⅱ. Rank order algorithm (ROC)
ⅲ. Direct cluster algorithm (DCA)
본문내용
1
1
1
1
1
5
1
1
1
1
1
1
MC-3
7
1
1
8
1
1
n _{1~} =~ {27} over {40}
n _{2~} =~ {75} over {77}
GE = 0.5
27 over 40
+ (1 - 0.5)
75 over 77
= 0.8245 (82.45%)
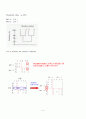
② machine이 4개 일 때 (Bottle neck이 2개)
PF-1
PF-2
PF-3
PF-4
1
6
4
10
5
2
3
7
8
9
11
12
13
MC-1
3
1
1
9
1
MC-2
7
1
1
8
1
1
MC-3
4
1
1
1
6
1
MC-4
1
1
1
1
1
1
1
1
2
1
1
1
1
1
5
1
1
1
1
1
1
n _{1~} =` {27} over {34}
n _{2~} =` {81} over {83}
GE = 0.5
27 over 34
+ (1 - 0.5)
81 over 83
= 0.8850 (88.5%)
machine을 세 개 두었을 때보다 네 개 두었을 때 효율이 더 높은 것을 알 수 있다.
ⅱ. Rank order algorithm (ROC)
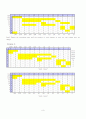
① row부터 sort했을 때 (Bottle neck이 1개)
row
6
1
7
8
12
2
3
9
13
11
10
5
4
256
3
1
1
0
0
0
0
0
0
0
0
0
0
0
6144
128
9
1
0
0
0
0
0
0
0
0
0
0
0
0
4096
64
1
0
0
1
1
1
1
1
1
1
0
0
0
0
2032
32
2
0
0
1
1
1
1
0
0
0
1
0
0
0
1928
16
5
0
0
1
1
1
0
1
1
1
0
0
0
0
1904
8
4
0
0
0
0
0
0
1
0
0
0
1
1
0
70
4
7
0
0
0
0
0
0
0
0
0
0
1
0
1
5
2
8
0
0
0
0
0
0
0
0
0
0
1
0
1
5
1
6
0
0
0
0
0
0
0
0
0
0
0
1
0
2
384
256
112
112
112
96
88
80
80
32
14
9
6
n sub 1
=
{28} over {40}
n sub 2
=
{ 76} over {77 }
GE = 0.5
28over40
+(1 - 0.5)
76over77
= 0.8435(84.35%)
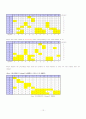
② column부터 sort했을 때 (Bottle neck이 3개)
4096
2048
1024
512
256
128
64
32
16
8
4
2
1
7
8
12
2
3
9
13
11
5
10
4
6
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
8128
2
1
1
1
1
0
0
0
1
0
0
0
0
0
7712
5
1
1
1
0
1
1
1
0
0
0
0
0
0
7616
4
0
0
0
0
1
0
0
0
1
1
0
0
0
280
6
0
0
0
0
0
0
0
0
1
0
0
0
0
16
7
0
0
0
0
0
0
0
0
0
1
1
0
0
12
8
0
0
0
0
0
0
0
0
0
1
1
0
0
12
3
0
0
0
0
0
0
0
0
0
0
0
1
1
3
9
0
0
0
0
0
0
0
0
0
0
0
1
0
2
n sub 1
=
{26} over {39}
n sub 2
=
{ 75} over {78}
GE = 0.5
26over39
+(1 - 0.5)
75over78
= 0.8141(81.41%)
두 번째 방법에서 GE는 81.41%로 이전보다 약 3% 감소했고, Bottle neck도 두 개 더 늘어났다. 즉, row부터 sort 했을 때가 column부터 sort 했을 때 보다 약 3% 증가 했고, Bottle neck도 두 개 더 적다.
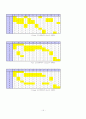
ⅲ. Direct cluster algorithm (DCA)
① Row 고정상태에서 Column의 재배열을 시작으로 한 재배열 (Bottle neck이 2개)
5
10
3
4
7
8
12
9
13
2
11
6
1
6
1
0
0
0
0
0
0
0
0
0
0
0
0
4
1
1
1
0
0
0
0
0
0
0
0
0
0
7
0
1
0
1
0
0
0
0
0
0
0
0
0
8
0
1
0
1
0
0
0
0
0
0
0
0
0
5
0
0
1
0
1
1
1
1
1
0
0
0
0
1
0
0
1
0
1
1
1
1
1
1
0
0
0
2
0
0
0
0
1
1
1
0
0
1
1
0
0
9
0
0
0
0
0
0
0
0
0
0
0
1
0
3
0
0
0
0
0
0
0
0
0
0
0
1
1
n sub 1
=
{27} over {41}
n sub 2
=
{ 74} over {76}
GE = 0.5
27over41
+(1 - 0.5)
74over76
= 0.8161(81.61%)
② Column 고정상태에서 Row의 재배열을 시작으로 한 재배열 (Bottle neck이 4개)
3
10
5
7
8
12
9
13
2
4
11
6
1
4
1
1
1
0
0
0
0
0
0
0
0
0
0
5
1
0
0
1
1
1
1
1
0
0
0
0
0
1
1
0
0
1
1
1
1
1
1
0
0
0
0
7
0
1
0
0
0
0
0
0
0
1
0
0
0
8
0
1
0
0
0
0
0
0
0
1
0
0
0
6
0
0
1
0
0
0
0
0
0
0
0
0
0
2
0
0
0
1
1
1
0
0
1
0
1
0
0
9
0
0
0
0
0
0
0
0
0
0
0
1
0
3
0
0
0
0
0
0
0
0
0
0
0
1
1
n sub 1
=
{25} over {69}
n sub 2
=
{ 44} over {48}
GE = 0.5
25over69
+(1 - 0.5)
44over48
= 0.6395(63.95%)
두 번째 방법에서 GE는 63.95%로 이전보다 약 18% 감소했고, Bottle neck도 두 개 더 늘어났다. 즉, Row 고정상태에서 Column의 재배열을 시작으로 한 재배열 Column 고정상태에서 Row의 재배열을 시작으로 한 재배열 했을 때 보다 약 18% 증가 했고, Bottle neck도 두 개 더 적다.
* 참고문헌 *
1. 강경식 외, GT 분석 이론에 관한 연구, 공학기술연구소 논문집, 1991
2. 이준한, 그룹 테크놀러지와 제조셀 형성방법에 대한 연구, 地域開發論叢, 1998
3. 이진구, GT를 이용한 일정계획에 관한 연구, 전남대학교, 1987
1
1
1
1
5
1
1
1
1
1
1
MC-3
7
1
1
8
1
1
n _{1~} =~ {27} over {40}
n _{2~} =~ {75} over {77}
GE = 0.5
27 over 40
+ (1 - 0.5)
75 over 77
= 0.8245 (82.45%)
② machine이 4개 일 때 (Bottle neck이 2개)
PF-1
PF-2
PF-3
PF-4
1
6
4
10
5
2
3
7
8
9
11
12
13
MC-1
3
1
1
9
1
MC-2
7
1
1
8
1
1
MC-3
4
1
1
1
6
1
MC-4
1
1
1
1
1
1
1
1
2
1
1
1
1
1
5
1
1
1
1
1
1
n _{1~} =` {27} over {34}
n _{2~} =` {81} over {83}
GE = 0.5
27 over 34
+ (1 - 0.5)
81 over 83
= 0.8850 (88.5%)
machine을 세 개 두었을 때보다 네 개 두었을 때 효율이 더 높은 것을 알 수 있다.
ⅱ. Rank order algorithm (ROC)
① row부터 sort했을 때 (Bottle neck이 1개)
row
6
1
7
8
12
2
3
9
13
11
10
5
4
256
3
1
1
0
0
0
0
0
0
0
0
0
0
0
6144
128
9
1
0
0
0
0
0
0
0
0
0
0
0
0
4096
64
1
0
0
1
1
1
1
1
1
1
0
0
0
0
2032
32
2
0
0
1
1
1
1
0
0
0
1
0
0
0
1928
16
5
0
0
1
1
1
0
1
1
1
0
0
0
0
1904
8
4
0
0
0
0
0
0
1
0
0
0
1
1
0
70
4
7
0
0
0
0
0
0
0
0
0
0
1
0
1
5
2
8
0
0
0
0
0
0
0
0
0
0
1
0
1
5
1
6
0
0
0
0
0
0
0
0
0
0
0
1
0
2
384
256
112
112
112
96
88
80
80
32
14
9
6
n sub 1
=
{28} over {40}
n sub 2
=
{ 76} over {77 }
GE = 0.5
28over40
+(1 - 0.5)
76over77
= 0.8435(84.35%)
② column부터 sort했을 때 (Bottle neck이 3개)
4096
2048
1024
512
256
128
64
32
16
8
4
2
1
7
8
12
2
3
9
13
11
5
10
4
6
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
8128
2
1
1
1
1
0
0
0
1
0
0
0
0
0
7712
5
1
1
1
0
1
1
1
0
0
0
0
0
0
7616
4
0
0
0
0
1
0
0
0
1
1
0
0
0
280
6
0
0
0
0
0
0
0
0
1
0
0
0
0
16
7
0
0
0
0
0
0
0
0
0
1
1
0
0
12
8
0
0
0
0
0
0
0
0
0
1
1
0
0
12
3
0
0
0
0
0
0
0
0
0
0
0
1
1
3
9
0
0
0
0
0
0
0
0
0
0
0
1
0
2
n sub 1
=
{26} over {39}
n sub 2
=
{ 75} over {78}
GE = 0.5
26over39
+(1 - 0.5)
75over78
= 0.8141(81.41%)
두 번째 방법에서 GE는 81.41%로 이전보다 약 3% 감소했고, Bottle neck도 두 개 더 늘어났다. 즉, row부터 sort 했을 때가 column부터 sort 했을 때 보다 약 3% 증가 했고, Bottle neck도 두 개 더 적다.
ⅲ. Direct cluster algorithm (DCA)
① Row 고정상태에서 Column의 재배열을 시작으로 한 재배열 (Bottle neck이 2개)
5
10
3
4
7
8
12
9
13
2
11
6
1
6
1
0
0
0
0
0
0
0
0
0
0
0
0
4
1
1
1
0
0
0
0
0
0
0
0
0
0
7
0
1
0
1
0
0
0
0
0
0
0
0
0
8
0
1
0
1
0
0
0
0
0
0
0
0
0
5
0
0
1
0
1
1
1
1
1
0
0
0
0
1
0
0
1
0
1
1
1
1
1
1
0
0
0
2
0
0
0
0
1
1
1
0
0
1
1
0
0
9
0
0
0
0
0
0
0
0
0
0
0
1
0
3
0
0
0
0
0
0
0
0
0
0
0
1
1
n sub 1
=
{27} over {41}
n sub 2
=
{ 74} over {76}
GE = 0.5
27over41
+(1 - 0.5)
74over76
= 0.8161(81.61%)
② Column 고정상태에서 Row의 재배열을 시작으로 한 재배열 (Bottle neck이 4개)
3
10
5
7
8
12
9
13
2
4
11
6
1
4
1
1
1
0
0
0
0
0
0
0
0
0
0
5
1
0
0
1
1
1
1
1
0
0
0
0
0
1
1
0
0
1
1
1
1
1
1
0
0
0
0
7
0
1
0
0
0
0
0
0
0
1
0
0
0
8
0
1
0
0
0
0
0
0
0
1
0
0
0
6
0
0
1
0
0
0
0
0
0
0
0
0
0
2
0
0
0
1
1
1
0
0
1
0
1
0
0
9
0
0
0
0
0
0
0
0
0
0
0
1
0
3
0
0
0
0
0
0
0
0
0
0
0
1
1
n sub 1
=
{25} over {69}
n sub 2
=
{ 44} over {48}
GE = 0.5
25over69
+(1 - 0.5)
44over48
= 0.6395(63.95%)
두 번째 방법에서 GE는 63.95%로 이전보다 약 18% 감소했고, Bottle neck도 두 개 더 늘어났다. 즉, Row 고정상태에서 Column의 재배열을 시작으로 한 재배열 Column 고정상태에서 Row의 재배열을 시작으로 한 재배열 했을 때 보다 약 18% 증가 했고, Bottle neck도 두 개 더 적다.
* 참고문헌 *
1. 강경식 외, GT 분석 이론에 관한 연구, 공학기술연구소 논문집, 1991
2. 이준한, 그룹 테크놀러지와 제조셀 형성방법에 대한 연구, 地域開發論叢, 1998
3. 이진구, GT를 이용한 일정계획에 관한 연구, 전남대학교, 1987










































소개글