철근 콘크리트 보의 휨 설계 2 기본 핵심 이론 (강도 설계법, 단철근보, T형보, 복철근보 휨 강도, 등)

본문내용

제 3장 보의 휨설계 (강도설계법) II
1. 단철근 직사각형보의 단면 해석
1.1 등가 응력 사각형의 깊이 계산
힘의 평형조건 을 만족시키기 위해서는 이어야 하므로
에서
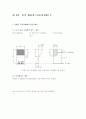
[그림] 강도 설계법에 의한 단철근보의 변형률도 및 응력도
1.2 공칭휨강도 계산
단면의 공칭휨강도=공칭휨모멘트 강도=내부의 우력 모멘트
또는 윗식에 C=T 로부터 유도된 a에 관한 식을 대입하면
1.3 설계 휨강도 계산
또는 라고 하면
1.4 계수(소요)휨강도의 비교
설계시에는 값 이상의 외부 휨모멘트가 작용해서는 안된다. 따라서 설계 휨강도 는 계수(소요) 휨강도 보다 커야 한다.
또한, 계산상 철근비 가 보다 크면 (즉, 이면, ) 로 보고 계산한다.
1.5 단철근 직사각형보의 단면설계 (단면이 주어지지않은 경우)
단면이 주어지지 않은 경우의 단면 설계를 등분포 하중을 받는 단순보에 적용해보면 다음과 같다.
(1) 설계하중 (=계수 하중)을 구한다.
(2) (계수) 휨강도(극한모멘트)를 구한다.
(3) 균형철근비
(4) 최대철근비
(5) 설계 휨강도를 구한다.
(6) 계수 휨강도와 설계 휨강도를 같다고 하여 콘크리트 단면의 폭 b와 높이 d를 구한다. 미지수가 둘이므로 보통 b는 가정하고 d를 계산한다.
,
(7) 철근량을 계산한다. (을 기본식으로 한다.)
(이 값은 최대 철근비에 의해서 구한 값이므로 최대값이 된다.)
(이 값은 에 의해 계산한 값보다 커서는 안된다.)
[그림] 단철근 보의 휨강도 계산 과정
2. 단철근 T형보의 단면해석
2.1 T형보의 판정과 유효폭
(1) 개설
교량이나 건물에서 슬래브와 보가 T형의 단일체가 되어 외력에 저항하도록 만들어진 구조를 T형보라고 한다.
[그림] 일방향 슬래브에서의 T형보
[그림] 철근콘크리트 거더교에서의 T형보
(2) T형보의 판정과 중립축의 위치 계산
T형보의 판정
a. 플랜지와 웨브의 경계면을 중립축으로 가정하고, 위쪽 플랜지의 단면 1차 모멘트 와, 아래쪽 인장철근의 환산 단면적의 단면 1차 모멘트 를 비교한다.
경계면이 중립축이라면 가 된다.
중립축이 플랜지쪽으로 올라가야 함
플랜지의 폭 b를 폭으로 하는 직사각형보
중립축이 웨브쪽으로 내려와야 함
T형보
b. 플랜지의 폭 b를 폭으로 하는 직사각형 단면의 도심축 x를 계산하여 플랜지 두께 와 비교한다.
플랜지의 폭 b를 폭으로 하는 직사각형보
T형보
중립축의 위치 계산
a. C=T에 의한 방법
b. 에 의한 방법
(3) 플랜지의 유효폭 (effective width)
T형보의 플랜지 폭은 웨브의 폭보다 크므로, 플랜지의 폭이 길어질수록 응력분포가 변한다. 따라서 응력 분포가 직사각형으로 일정하다고 볼 수 있는 플랜지 구간을 플랜지의 유효폭이라 한다.
[그림] T 형보의 유효폭
● 플랜지의 유효폭(b)의 계산
a. 대칭 T형 단면
다음 세 값 중에서 작은 값을 취한다.
-
- 양쪽 슬래브의 중심간 거리 =
- 보의 경간의 1/4 =
b. 비대칭 T형 단면
다음 세 값 중에서 작은 값을 취한다.
-
- (보의 경간의 1/12) +
- (인접보와의 내측 거리 의 1/2) +
c. 독립 T형보
플랜지의 두께는 복부폭의 1/2 이상이어야 하고, 플랜지 유효폭은 복부폭의 4배 이하이어야 한다.
2.2 중립축의 위치 c와 T형보의 판정
(1) 중립축의 위치
, , , ,
(2) T형보의 판정
T형보가 되기 위해서는 압축 휨응력을 받는 부분의 형태가 T형이어야 하므로 이어야 한다. 따라서 위 식에 의해 계산된 c값이 값보다 크면 T형보이고, 작으면 폭이 b인 직사각형보가 된다.
-> T형보
-> 폭이 b인 직사각형보
또는 응력의 깊이 a를 계산하여 와 비교해도 된다.
-> T형보
-> 직사각형보
직사각형 단면이라고 생각할 때의 a값 -> T형보 판정에 필요한 값
->
2.3 공칭휨강도 계산
(1) 플랜지 부분과 복부 부분을 구분하여 생각해보면 이므로
와 에 의한 공칭 저항 모멘트 (=)은 다음과 같다.
(2) 이므로
(3) 이므로
2.4 설계휨강도 계산
2.5 계수(소요) 휨강도 와 비교 검토
가 성립되는지를 검토하고, 성립되지 않으면 단면을 조정한다.
[그림] T 형보의 단면 해석
[그림] 압축응력 블록이 플랜지내에 있을 경우
[그림] 압축응력 블록이 복부내에 있을 경우
2.6 단철근 T형보의 단면 설계 (단면이 주어지지 않은 경우)
(1) 최대 철근비
여기서, ,
(2) 소요 철근량 계산
T형보는 보통 콘크리트의 단면 b, d가 주어지고 철근량을 구하게 된다.
따라서, 철근량 는 에 의해서 구하게 된다.
여기서,
를 알아야 a값이 계산되므로 처음에는 a를 0.9d 또는 로 가정하여, 가정값이 일치될 때까지 반복 계산한다. 이 때 가 최대 철근비 를 넘지 않도록 한다.
만약 플랜지 부분에 해당되는 철근량 가 필요하면, 에 의하여 이므로
3. 복철근 직사각형보의 단면 해석
3.1 복철근보로 하는 이유
단면의 치수(보의 깊이)가 제한되어 단철근보로서는 외력에 의한 작용 모멘트를 견딜 수 없는 경우
정(+), 부(-) 휨모멘트를 교대로 받을 경우
처짐을 극소화시켜야 할 경우
[그림] 단철근보와 복철근보의 비교
압축철근을 배치하는 이유
a. 지속하중에 의한 처짐을 감소시킴
b. 연성을 증가시킴
c. 파괴모드를 압축파괴에서 인장파괴로 유도함
d. 철근의 배치를 용이하게 함
3.2 등가 응력 사각형의 깊이 a 계산
단철근보에 의한 휨모멘트 이 외력에 의한 휨모멘트 보다 작으면 복철근보로 만들어 모자라는 휨모멘트 를 생성시킨다. 따라서 복철근보의 총응력은 그림에서 가 성립되므로
이므로
, 로 놓으면
3.3 공칭휨강도 계산
압축쪽의 총응력은 ‘콘크리트 총응력 ’과 ‘압축 철근의 총응력 ’의 2몫이 있으므로, 인장 철근의 총응력도 두 몫으로 분해 할 수 있다.
(1) 압축 콘크리트의 총응력 과 이에 해당하는 인장철근의 총응력 에 의한 우력모멘트 은
또는
(2) 압축 철근의 총응력 와 이에 해당하는 인장 철근의 총응력 에 의한 우력모멘트 는
(3) 공칭 휨강도
(4) 설계 휨강도 계산
[그림] 복철근 직사각형보의 단면 해석

키워드

철근,   콘크리트,   단철근,   복철근,   T형보,   유효폭,   강도,   설계