쉽게 배우는 알고리즘 총1-12 연습문제

본문내용

l을 부여한다(앞에서 한번 사용한 label과는 다른 값을 사용해야 한다). 아래 그림은 labeling의 한 예를 보인다. 두 정점에 인접한 정점들의 label의 조합이 같으면({i, j, k}와 {i, k, j})) 같은 label(r)이 부여된 예를 보이고 있다.
이런 식으로 모든 level에 대해 label 작업을 한다. 최종적으로 모든 level에서 두 트리의 정점 수가 같고 각 정점들의 label을 크기순으로 나열했을 때 같은 순열이 되면 두 트리는 동형이다. 위 작업은 다항식 시간에 이루어진다. 그러므로 ISP는 NP이다.
(ISP의 대답이 Yes라는 근거로 부분 그래프에 더하여 일대일 대응함수 까지 제공될 수도 있다. 이 경우에는 확인 방법이 trivial하다. 다항식 시간 변환에 초점을 맞추기 위해서는 이 방법이 더 나을 것이다.)
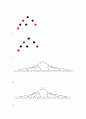
2) HAM-PATH 사례의 그래프 G=(V, E)와 |V| 개의 정점을 가진 체인형 트리 T를 ISP 사례로 사용한다. 이 사례를 만드는 것은 다항식 시간에 가능하다. 아래 그림은 |V|가 9인 체인형 트리를 예로 보인다.
그래프 G가 그래프가 T와 동형인 부분그래프를 갖는지 질문한다. 이 질문에 대한 대답이 Yes이면 그래프 G는 해밀토니안 경로를 갖는다. 대답이 No이면 해밀토니안 경로를 갖지 않는다. 그러므로 HAM-PATH는 ISP로 다항식 시간 변환가능하다.
위 1), 2)로부터 ISP는 NP-완비다.
9.
1) G에서 H와 동형인 부분 그래프와 일대일 대응 함수 가 주어질 때 이 두 그래프가 동형임을 확인하는 것은 다항식 시간에 가능하다. 그러므로 SUBGRAPH-ISOMOPHISM은 NP이다.
2) CLIQUE의 사례 그래프 G=(V, E)와 정수 K가 주어지면 그래프 G는 그대로 사용하고 이에 더하여 크기가 K인 완전 그래프 C를 하나 만든다. 이것을 SUBGRAPH-ISOMOPHISM의 사례로 사용한다. 즉, 변환은 의 시간이면 충분하다. SUBGRAPH-ISOMOPHISM에서 아래와 같이 질문한다.
“G가 C와 동형인 부분 그래프를 포함하는가?”
이 질문에 대한 대답과 CLIQUE의 질문 “G가 크기 K인 완전 부분 그래프를 포함하는가?”에 대한 대답은 일치한다. 그러므로 CLIQUE은 SUBGRAPH-ISOMOPHISM으로 다항식 시간 변환 가능하다.
위 1), 2)로부터 SUBGRAPH-ISOMOPHISM은 NP-완비다.
10.
1) BIN-PACKING의 질문에 Yes라고 대답할 수 있는 근거로 부분 집합 가 주어지면 각 집합에 속한 항목들의 합이 B를 초과하지 않음을 확인하는 것은 선형시간에 가능하다. 그러므로 BIN-PACKING은 NP이다.
2) PARTITION의 사례가 주어지면 다음과 같이 BIN-PACKING의 사례를 만든다.
U=A, PARTITION의 각 원소 a는 BIN-PACKING의 한 항목이 된다. K=2로 잡고, B는 모든 항목의 합을 2로 나눈 수로 잡는다. 이것이 BIN-PACKING의 사례가 된다. 이 변환은 항목의 수에 대한 선형시간이면 된다. BIN-PACKING에서 아래와 같이 질문한다.
“U를 2개의 상호배타적인 집합 로 분할하되 각 집합이 B를 초과하지 않는 방법이 존재하는가?”
이 질문에 대한 대답과 원래의 PARTITION 사례의 질문에 대한 대답은 일치한다. 그러므로 PARTITION은 BIN-PACKING으로 다항식 시간 변환가능하다.
위 1), 2)로부터 BIN-PACKING은 NP-완비다.
11. 8절에서 보인 바와 같이 삼각부등식을 만족하면 최적해의 3/2배를 초과하지 않는 해를 구할 수 있다. 도시들간의 거리가 1부터 100 사이이면서 삼각부등식을 만족하지 않는 사례에서 모든 간선에 98을 더하면 삼각부등식을 만족하게 된다. 이렇게 변환하면 모든 해는 원래 사례의 해보다 만큼 크다(n은 정점의 총 수). 따라서 최적해 C에 대응되는 해는 이 된다. 근사 비율 3/2를 보장하는 알고리즘이 있으므로 이를 이용해서 을 초과하지 않은 해를 구할 수 있다. 여기서 을 빼면 이 된다. 주어진 TSP 문제에서 어떤 경우든 최적해 C보다 이상 크지 않은 해를 구할 수 있다.
12장
1~6. 생략
7. 잃는 점: 최적해를 보장할 수 없다.
얻는 점: 잔여거리보다 작은 것을 보장하기 위해 추정치와 실제잔여치의 차이가 필요 이상으로 커질 가능성이 많다. 잔여거리보다 작은 것이 보장되지는 않지만 잔여거리를 더 정확히 추정할 수 있는 수단이 있으면 최적해는 보장하지 못하지만 탐색은 더 빠르고 효율성은 높아질 것이다.
실제 잔여거리보다 작은 추정값을 구할 수 없을 때, 잔여거리보다 작은 것이 보장되지 않는 추정값이라도 쓰면 근사해를 구할 수 있다. (잔여거리의 추정치를 무조건 0으로 놓으면 실제 잔여거리보다 작은 추정값으로 삼을 수는 있으나 아무 의미없는 추정치라 탐색의 품질에 도움을 주지 못한다. 이럴 때 잔여거리보다 작은 것이 보장되지는 않지만 잔여거리를 추정할 수 있는 수단이 있으면 그것을 사용하는 것이 더 나을 수 있다. 물론 추정의 합리성에 따라 품질은 영향을 받겠지만...)
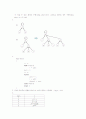
8. 본문에서 사용한 방식은 설명의 간명함을 위해 추정치를 정적으로 구하는 방식이다. 즉, 각 정점에서 다른 정점들에 이르는 간선들 중 가장 짧은 것을 초기에 한 번 구해 놓은 다음 이후에는 어떤 상황이든 이것을 해당 정점과 관계된 추정치로 삼는다. 이것은 지금까지 탐색해온 상황을 고려하지 않으므로 다소 낭비가 있다. 예를 들어 [그림 12-8]에서 11번 노드의 1-3-4를 보면 추정 잔여거리가 16이다. 이것은 3(정점 4)+10(정점 2)+3(정점 5)에 의해 계산된 것이다. 그런데 정점 5와 관계된 값 3은 정점 4로 연결될 때 가능한 값이다. 그렇지만 정점 4는 이미 정점 3으로부터 연결되어 있으므로 정점 5 다음에 4를 방문할 수는 없다. 정점 5 다음에 방문할 가능성이 남아있는 정점은 1, 2 뿐이다. 그러므로 정점 5와 관계된 추정치로는 10이 최선이다. 이를 이용해서 1-3-4의 추정치를 추정하면 17+23=40이 된다. 33보다 더 실제치에 가까운 추정치이다.

키워드

1,   2,   3