무한급수

목차

없음

본문내용

수학은 컴퓨터 없이는 탄생할 수 없었던 수학이다. 수학이 컴퓨터를 발전시킨다고 봐야 하는가? 아니면 컴퓨터가 수학을 발전시킨다고 봐야 하는가? 둘 모두 맞는 답이다.
오늘날, 컴퓨터를 이용하는 현대수학 특히 비선형 수학에서 다루는 문제들은 굉장히 복잡하고 또 고교수학 수준에서 이해하기 어려운 것들이 많으므로, 컴퓨터가 수학문제 해결 혹은 이해에 도움이 되는 한 예를 바로 위의 문제를 통해 보기로 하자.
자연수의 역수를 차례로 더해 가는 위의 문제를 수학식으로 표현하면 다음과 같다. (식이라는 것에 대해 너무 부정적 인식을 갖지 말기를.)

세상에 등장한 컴퓨터 가운데 무한을 처리할 수 있는 수준의 것은 아직까지 없다. 그러므로 컴퓨터를 이용해 위의 문제를 접근하기 위해서는 합산기호 위의 무한대 기호를 적당한 유한크기의 숫자로 대치해야 한다. 위의 문제를 컴퓨터에 실행시킬 만한 논리식으로 표현하면 다음과 같다.
Get Number
S = 0
Do I = 1, Number
S = S + 1/i
Loop
즉, 사용자가 일정 크기의 자연수(Number)를 지정해 주면, "1+1/2+1/3+...+1/Number"를 컴퓨터로 하여금 수행하게끔 하는 논리식이다. 본 예제에서는 시간관계상 2천8백만 번까지만 수행하였다.
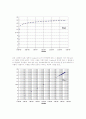
위의 그림에서 보면, 입력치 Number의 크기가 증가함에 따라 그 결과값이 마치 어떤 값으로 수렴할 것처럼 보인다. 그러나 사실은 그렇지 않다. Number의 증가에 따라 그 결과값 S도 끊임없이 증가한다. 위와 같은 단순 직교좌표계로써는 S의 증가성을 한 눈에 파악하기가 어렵다. (정말이지, 수렴할 것처럼 보인다.) 하지만, 다음의 그림을 보면...

위 그림은 동일한 결과에 대해 X축을 Log Scale로 표현한 것이다. (점점 머리가 아파질지도 모르겠으나 참고, 보고, 배우고 깨닫는 데 수학의 매력이 있다. 세상 모든 학문이 또한 그러하며, 세상을 산다는 자체가 그러하다.)
그 결과는 분명한 하나의 경향성 즉, 직선으로 뻗어 올라가는 경향성을 보여준다. 사실 이 답이 무한으로 가는 것임은 이미 증명했으나 본 예제는 컴퓨터가 어떻게 수학에 도움이 되는가를 보여주기 위한 것임을 상기하기 바란다. 그리고 바로 이 순간 로그 스케일의 이해가 가지 않는다면 그냥 넘어가기 바란다. 로그 스케일을 이해하고자 하는 대목이 아니기 때문이다. 어쨌거나 더하는 횟수의 크기만 문제될 뿐 그 방향성은 분명히 직선으로 뻗어 있다.
복잡계 해석 등과 같은 최신 수학에서는 위와 유사한 방식으로 컴퓨터를 활용하고 있다. 손이나 머리로는 쉽게 풀리지 않는 수학 문제들(혹은 모델링)을 수치해석이라는 컴퓨터 활용기법을 동원해서 그 현상을 먼저 탐구해보고 나중에 수학적 엄정함을 갖추는 식으로 활용하는 것이다. 단, 순수 수학이 아닌 응용공학 분야에서는 답의 이해를 구하는 과정까지는 가지 않고 다만 현상을 파악하는데 그친다. 왜냐하면 공학문제를 해결하는데 있어서 그 정도면 충분하기 때문이다.

키워드

무한급수,   무한급수 사례,   무한급수의 예