
-
1
-
2
-
3
-
4
-
5
-
6
-
7
-
8
-
9
-
10
-
11
-
12
-
13
-
14
-
15
-
16
-
17
-
18
-
19
-
20
-
21
-
22
-
23
-
24
-
25
-
26
-
27
-
28
-
29
-
30
-
31
-
32
-
33
-
34
-
35
-
36
-
37
-
38
-
39
-
40
-
41
-
42
-
43
-
44
-
45
-
46
-
47
-
48
-
49
-
50
-
51
-
52
-
53
-
54
-
55
-
56


목차
제1절 수익률곡선 개념
제2절 수익률의 개념과 종류
1. 할인함수와 현물이자율
2. 일물일가의 법칙
3. 만기수익률
4. 보유기간 수익률
5. 여타 채권수익률의 표시방법
6. 선도이자율
7. 국내 주요채권 가격 계산방법의 실례
제3절 수익률 결정에 관한 이론
1. 이자율 결정이론
2. 수익률 기간구조에 관한 이론
제4절 채권위험의 측정
1. 듀레이션
2. 컨벡시티
제2절 수익률의 개념과 종류
1. 할인함수와 현물이자율
2. 일물일가의 법칙
3. 만기수익률
4. 보유기간 수익률
5. 여타 채권수익률의 표시방법
6. 선도이자율
7. 국내 주요채권 가격 계산방법의 실례
제3절 수익률 결정에 관한 이론
1. 이자율 결정이론
2. 수익률 기간구조에 관한 이론
제4절 채권위험의 측정
1. 듀레이션
2. 컨벡시티
본문내용
.000
1.00
0.944
0.976
0.992
1.000
1.50
0.914
0.950
0.966
0.969
1.000
2.00
0.847
0.887
0.908
0.915
0.975
1.000
2.50
0.796
0.840
0.860
0.870
0.948
0.989
1.000
3.00
0.749
0.789
0.815
0.829
0.908
0.955
0.971
1.000
5.00
0.712
0.751
0.776
0.788
0.871
0.912
0.933
0.952
1.000
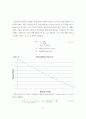
채권의 가격변동위험은 듀레이션 뿐만 아니라 이자율의 변동성에 의해서도 영향을 받지만 듀레이션에 의한 가격변동성의 측정은 이점을 고려하지 않는다. 예를 들어 이자율이 8%인 경우 3개월 만기 무이표채권과 5년 만기 무이표채권의 듀레이션을 계산하면 각각 0.245, 4.90의 값이 되는데 이는 5년 만기 채권의 위험이 3개월 만기 채권의 위험에 비해 20배 더 큰 것을 의미한다. 하지만 이것이 가격변동율 측면에서 반드시 5년 만기 무이표채의 위험이 20배 더 크다는 것을 의미하지는 않는다. 예를 들어 (식 I-20)의 공식으로부터 가격 변동율의 표준편차는
Std LEFT ( { TRIANGLE P} over {P } RIGHT ) = D TIMES Std LEFT (TRIANGLE y RIGHT )
과 같이 표현할 수 있다. 즉 1년 만기 무이표채의 가격 변동율 표준편차는
0.245 times 0.223=0.054728%
, 5년 만기 무이표채의 가격 변동율 표준편차는
4.90 times 0.309=1.51370%
로 가격 변동율 측면에서는 5년 만기 채권이 27배 정도 더 위험하다.
특히 채권 포트폴리오의 경우 이자율간의 상관관계 혹은 공분산이 채권 포트폴리오의 위험을 측정하는데 중요한 요소가 된다. 채권 포트폴리오의 가치를 Pp로 표기하면 다음과 같은 선형추정방식(linearization)을 통해 포트폴리오의 가치 변동분을 근사치로 구해낼 수 있다.
{ {p\' }_{p }- {p }_{p } } over { { p}_{p } } APPROX - { D}_{k1}( {y }_{k\'1 }- {y }_{k1 } ) }- { D}_{k2 }( { y}_{k\'2 }- { y}_{k2 })
(식 I-47)
yk1, yk2 : 가장 영향력이 크다고 여겨지는 주요 수익률(key rates)
따라서 포트폴리오의 실효수익률 분산은 다음의 (식 I-48)과 같은 방식으로 근사치를 구해낼 수 있다. 이는 포트폴리오 실효수익률의 위험 측정치인 분산이 주요 현물이자율(key-rate)에 대한 듀레이션 뿐만 아니라 주요 현물이자율 사이의 공분산에도 영향을 받는다는 것을 알 수 있다.
Var LEFT ( { { p\'}_{p }- { p}_{p } } over { { p}_{p } } RIGHT ) APPROX { D}`_{k1 } ^{2 } { sigma }`_{k1 } ^{2 }+ { D}`_{k2 } ^{2 } { sigma }`_{k2 } ^{2 }+2 { D}_{k1 } { D}_{k2 } { sigma }`_{k1,k2 } ^{2}
(식 I-48)
σ2k1, σ2k2, : 주요 수익률(key rate)의 분산(variance)
σ2k1,k2 : 주요 수익률의 공분산(covariance)
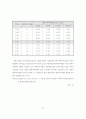
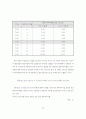
실제 1998 9월 2일부터 2000년 7월 5일 동안의 산금채의 시가평가기준수익률의 주간 변동치(
TRIANGLE y
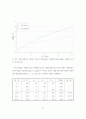
)를 이용하여 RiskMetrics 방법에 의해 상관관계를 구해 보면 (그림 I-11)과 같다. RiskMetrics 방법에서는 시간가변 변동성과 공분산성을 (식 I-49)과 같은 방법으로 구한다.
sigma_{i,t+1}^2 = lambda sigma_{i,t}^2 + (1-lambda) epsilon_{i,t}^2
sigma_{i,j,t+1} = lambda sigma_{i,j,t} + (1-lambda) epsilon_{i,t} epsilon_{j,t}
(식 I-49)
(그림 I-11)에서의 값은
lambda
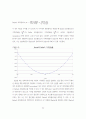
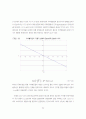
의 값을 0.9로 하여 구한 것이다. RiskMetrics 방법은 과거 자료의 분산 및 공분산의 예측을 위해 과거 자료의 비중을 지수가중(exponential weight)을 이용하여 구하는 방법으로 GARCH(generalized autoregressive conditional heteroscedasticity) 모형에서 보면 IGARCH(1,1) 모형과 동일하다. 그림에서 알 수 있듯이 현물이자율 간의 상관관계는 일정하기 보다는 시간에 가변(time-varying)하는 속성을 가지고 있는데 예를 들어 3개월 현물이자율과 5년 현물이자율 간의 상관관계는 0.6에서 0.85사이에서 변동하였음을 알 수 있다. 이는 전통적인 듀레이션 방법에 따른 채권 포트폴리오의 위험측정 방법은 수익률곡선의 변동이 평행이동 한다는 가정을 통해 상관관계를 무시하고 더욱이 상관관계의 가변성을 무시한다는 점에서 문제점을 내포하고 있음을 의미하는 것이다.
전술한 RiskMetrics 방법은 JP Morgan이 제시하고 있는 방법으로 분산 및 공분산 혹은 상관관계의 추정은 쉽게 과거자료를 이용하여 추정치를 구함으로써 금융기관의 위험관리(risk management)에 쉽게 적용할 수 있는 장점이 있다.
) 실제 JP Morgan 공표하는 분산 공분산 추정치는 이자율의 증분 즉
TRIANGLE y= { y}_{t }- { y}_{t-1 }
에 기초한 것이 아니라 이자율의 변동률, 즉
{ { y}_{t }- { y}_{t-1 } } over { { y}_{t-1 } }
에 기초한 추정치이기 때문에 사용에 주의를 하여야 한다.
하지만 RiskMetrics 방법은 분산 및 공분산 예측을 위한 하나의 방법에 불과하며, 채권 포트폴리오의 위험관리에 듀레이션과 통계적 방법을 결합한 방법을 사용하기 위해서는 보다 정교한 통계적 모형에 대한 분석이 요구된다.
(그림 I-11) RiskMetrics방법에 의한 산금채 수익률 변동치의 상관관계
1.00
0.944
0.976
0.992
1.000
1.50
0.914
0.950
0.966
0.969
1.000
2.00
0.847
0.887
0.908
0.915
0.975
1.000
2.50
0.796
0.840
0.860
0.870
0.948
0.989
1.000
3.00
0.749
0.789
0.815
0.829
0.908
0.955
0.971
1.000
5.00
0.712
0.751
0.776
0.788
0.871
0.912
0.933
0.952
1.000
채권의 가격변동위험은 듀레이션 뿐만 아니라 이자율의 변동성에 의해서도 영향을 받지만 듀레이션에 의한 가격변동성의 측정은 이점을 고려하지 않는다. 예를 들어 이자율이 8%인 경우 3개월 만기 무이표채권과 5년 만기 무이표채권의 듀레이션을 계산하면 각각 0.245, 4.90의 값이 되는데 이는 5년 만기 채권의 위험이 3개월 만기 채권의 위험에 비해 20배 더 큰 것을 의미한다. 하지만 이것이 가격변동율 측면에서 반드시 5년 만기 무이표채의 위험이 20배 더 크다는 것을 의미하지는 않는다. 예를 들어 (식 I-20)의 공식으로부터 가격 변동율의 표준편차는
Std LEFT ( { TRIANGLE P} over {P } RIGHT ) = D TIMES Std LEFT (TRIANGLE y RIGHT )
과 같이 표현할 수 있다. 즉 1년 만기 무이표채의 가격 변동율 표준편차는
0.245 times 0.223=0.054728%
, 5년 만기 무이표채의 가격 변동율 표준편차는
4.90 times 0.309=1.51370%
로 가격 변동율 측면에서는 5년 만기 채권이 27배 정도 더 위험하다.
특히 채권 포트폴리오의 경우 이자율간의 상관관계 혹은 공분산이 채권 포트폴리오의 위험을 측정하는데 중요한 요소가 된다. 채권 포트폴리오의 가치를 Pp로 표기하면 다음과 같은 선형추정방식(linearization)을 통해 포트폴리오의 가치 변동분을 근사치로 구해낼 수 있다.
{ {p\' }_{p }- {p }_{p } } over { { p}_{p } } APPROX - { D}_{k1}( {y }_{k\'1 }- {y }_{k1 } ) }- { D}_{k2 }( { y}_{k\'2 }- { y}_{k2 })
(식 I-47)
yk1, yk2 : 가장 영향력이 크다고 여겨지는 주요 수익률(key rates)
따라서 포트폴리오의 실효수익률 분산은 다음의 (식 I-48)과 같은 방식으로 근사치를 구해낼 수 있다. 이는 포트폴리오 실효수익률의 위험 측정치인 분산이 주요 현물이자율(key-rate)에 대한 듀레이션 뿐만 아니라 주요 현물이자율 사이의 공분산에도 영향을 받는다는 것을 알 수 있다.
Var LEFT ( { { p\'}_{p }- { p}_{p } } over { { p}_{p } } RIGHT ) APPROX { D}`_{k1 } ^{2 } { sigma }`_{k1 } ^{2 }+ { D}`_{k2 } ^{2 } { sigma }`_{k2 } ^{2 }+2 { D}_{k1 } { D}_{k2 } { sigma }`_{k1,k2 } ^{2}
(식 I-48)
σ2k1, σ2k2, : 주요 수익률(key rate)의 분산(variance)
σ2k1,k2 : 주요 수익률의 공분산(covariance)
실제 1998 9월 2일부터 2000년 7월 5일 동안의 산금채의 시가평가기준수익률의 주간 변동치(
TRIANGLE y
)를 이용하여 RiskMetrics 방법에 의해 상관관계를 구해 보면 (그림 I-11)과 같다. RiskMetrics 방법에서는 시간가변 변동성과 공분산성을 (식 I-49)과 같은 방법으로 구한다.
sigma_{i,t+1}^2 = lambda sigma_{i,t}^2 + (1-lambda) epsilon_{i,t}^2
sigma_{i,j,t+1} = lambda sigma_{i,j,t} + (1-lambda) epsilon_{i,t} epsilon_{j,t}
(식 I-49)
(그림 I-11)에서의 값은
lambda
의 값을 0.9로 하여 구한 것이다. RiskMetrics 방법은 과거 자료의 분산 및 공분산의 예측을 위해 과거 자료의 비중을 지수가중(exponential weight)을 이용하여 구하는 방법으로 GARCH(generalized autoregressive conditional heteroscedasticity) 모형에서 보면 IGARCH(1,1) 모형과 동일하다. 그림에서 알 수 있듯이 현물이자율 간의 상관관계는 일정하기 보다는 시간에 가변(time-varying)하는 속성을 가지고 있는데 예를 들어 3개월 현물이자율과 5년 현물이자율 간의 상관관계는 0.6에서 0.85사이에서 변동하였음을 알 수 있다. 이는 전통적인 듀레이션 방법에 따른 채권 포트폴리오의 위험측정 방법은 수익률곡선의 변동이 평행이동 한다는 가정을 통해 상관관계를 무시하고 더욱이 상관관계의 가변성을 무시한다는 점에서 문제점을 내포하고 있음을 의미하는 것이다.
전술한 RiskMetrics 방법은 JP Morgan이 제시하고 있는 방법으로 분산 및 공분산 혹은 상관관계의 추정은 쉽게 과거자료를 이용하여 추정치를 구함으로써 금융기관의 위험관리(risk management)에 쉽게 적용할 수 있는 장점이 있다.
) 실제 JP Morgan 공표하는 분산 공분산 추정치는 이자율의 증분 즉
TRIANGLE y= { y}_{t }- { y}_{t-1 }
에 기초한 것이 아니라 이자율의 변동률, 즉
{ { y}_{t }- { y}_{t-1 } } over { { y}_{t-1 } }
에 기초한 추정치이기 때문에 사용에 주의를 하여야 한다.
하지만 RiskMetrics 방법은 분산 및 공분산 예측을 위한 하나의 방법에 불과하며, 채권 포트폴리오의 위험관리에 듀레이션과 통계적 방법을 결합한 방법을 사용하기 위해서는 보다 정교한 통계적 모형에 대한 분석이 요구된다.
(그림 I-11) RiskMetrics방법에 의한 산금채 수익률 변동치의 상관관계
키워드
추천자료
 [사회과학] 지역격차의 자료분석과 이해 - 미국의 1990년, 2000년 주별 자료
[사회과학] 지역격차의 자료분석과 이해 - 미국의 1990년, 2000년 주별 자료 지역격차의 자료분석과 이해 - 미국의 1990년, 2000년 주별 자료
지역격차의 자료분석과 이해 - 미국의 1990년, 2000년 주별 자료 토목기사 실기 요약정리
토목기사 실기 요약정리 국내외균형과 정책수단 할당
국내외균형과 정책수단 할당 리플 메서드( Ripple's method )
리플 메서드( Ripple's method ) 수요 공급 이론에 의한 금리 결정 요인
수요 공급 이론에 의한 금리 결정 요인 체인지몬스터를 읽고
체인지몬스터를 읽고 탄성계수, 단면수축율, 연신율, 항복응력, 인장강도 계산법
탄성계수, 단면수축율, 연신율, 항복응력, 인장강도 계산법 [계량경제학]소득변화에 따른 곡물소비량분석
[계량경제학]소득변화에 따른 곡물소비량분석 DC B-H LOOP 측정
DC B-H LOOP 측정 입도분포시험-체분석[압밀실험]
입도분포시험-체분석[압밀실험] 토질역학2 및 실습, 흙의 입도분석시험(R-1)(A+자료임.)
토질역학2 및 실습, 흙의 입도분석시험(R-1)(A+자료임.) 7. 고분자전해질 연료전지(PEMFC) 및 직접메탄올 연료전지(DMFC) 성능 실험과 분해조립
7. 고분자전해질 연료전지(PEMFC) 및 직접메탄올 연료전지(DMFC) 성능 실험과 분해조립 [이문화연구 관련 해석] 한계효용체감사례 통한 글로브 연구 가치와 관행 해석 - GLOBE 관행...
[이문화연구 관련 해석] 한계효용체감사례 통한 글로브 연구 가치와 관행 해석 - GLOBE 관행...



































































소개글