Matlab을 이용한 AM, FM 변조기 및 복조기 구현

소개글

Matlab을 이용한 AM, FM 변조기 및 복조기 구현에 대한 보고서 자료입니다.

목차

1.AM 의 변조기 및 복조기의 생성 원리설명
2.FM의 변조기 및 복조기의 생성 원리 설명
3.matlab 소스 코드
4.매틀랩 소스코드에 음원을 통과시켜 SNR 분석
5.결과파형

본문내용

백색잡음 전력을 정의
N_std = sqrt(N); %백색잡음 전력을 이용하여 백색잡음의 표준편차를 구함.
Nt = N_std.*randn(1,length(s_m)); %st의 구간동안 표준편차 N_std으로 백색잡음 생성.
st_awgn = s_m+Nt; %백색잡음이 포함된 변조신호 st_awgn
St_awgn_f = 1/Fs*fft(st_awgn, length(st_awgn)); %$변조신호 st_awgn의 푸리에 변환
%S_fb = St_awgn_f.*Hf; 필터로 필터링된 신호 YfL
%s_mb = real(ifft(S_fb))*Fs; 저역통과 필터로 필터링된 신호 YfL를 시간영역으로 역푸리에 변환
%signal demodulation
pre_nqt=Nt.*(-2*sin(2*pi*Fc.*t')); %잡음 Nt와 sin함수의 곱
PRE_NQT=1/Fs*fft(pre_nqt,length(pre_nqt));%/Fs; pre_nqt의 푸리에 변환
h=2*Fm*sinc(2*Fm.*t); %sinc함수를 이용하여 h 설정
%NQT=H.*PRE_NQT; 주파수 도메인에서 곱 (시간 도메인에서 convolution 역할)
nqt=ifft(PRE_NQT,length(PRE_NQT))/(2*pi); % NQT의 역푸리에 변환하여 LPF로 필터링 된 nqt signal완성
ndt1=diff(nqt)/(2*pi); %nqt 미분
ndt=[ndt1,0];
v=kf.*m+ndt'; %signal에 잡음을 더해준다
Vf=1/Fs*fft(v,length(v));
fm1=conv(v,h);
fm=fm1(length(m)/2:(length(m)+(length(m)/2-1)));
FM=1/Fs*fft(fm,length(fm));
% i=1:length(m);
% delta = m(i)-fm(i);
% sqdelta=delta.^2;
% mse=mean(sqdelta)
%
wavwrite(fm,Fs*5,'fm_+10dB.wav'); %save result as output file
f=-1/2*length(M):1/2*length(M)-1;
t1 = 1/(10*Fs)*[0 :length(m)-]'; %define the range of time domain
f1=-1*length(M):length(M)-1;
figure(1);
subplot(1,2,1);plot(t,m,'r');title('m(t) message signal'); xlabet('time');ylabel('m(t)');
hold on
subplot(1,2,2);plot(t,fm,'b');title('fm(t) fm modulated signal'); xlabet('time');ylabel('fm(t)');
figure(2);
subplot(1,2,1);plot(f,M,'r');title('M(f) message signal'); xlabet('time');ylabel('m(t)');
hold on
subplot(1,2,2);plot(f,FM,'b');title('FM(f) message signal'); xlabet('time');ylabel('m(t)');
subplot(2,2,4)
plot(f,FM,'b');title('FM(f) message signal'); xlabet('time');ylabel('m(t)');
3. 결과 그래프
** 자세한 그래프 하나하나에 대해서는 noise 추가 전의 것과 입력 SNR 10dB를 기준한 것 이 두 가지에 대한 것입니다.
대표적인 세 경우 입력 SNR= 10, 0, -10dB에 대해서 한 눈에 볼 수 있도록 그래프도 첨부했습니다.
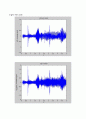
ㄱ. DSB-SC
대조군: noise를 첨가하지 않았을 때.
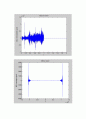
입력 SNR=10dB
한눈에 보면:
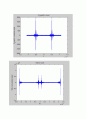
입력 SNR=0dB
입력 SNR=-10dB
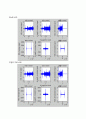
ㄴ. FM
대조군: noise를 첨가하지 않은 변복조 결과 파형.
입력 SNR=10dB
입력 SNR=-10dB
4. 성능 분석
AWGN 채널을 적용한다는 것은 가 변조된 신호 s(t)에 더해지는 시스템을 구현했다는 의미이다. DSB-SC와 FM 변복조기를 구현할 때 사용된 신호들을 이용하여 신호 대 잡음비 성능 분석을 수행하고, 이론적인 성능과 비교해 보자.
1) DSB-SC(AM)
먼저, 변조된 신호 이고,
output signal의 power P는, 이다.
->
Noise Power = 이다.
또한, 우리 팀이 구현한 시스템의 Ac=1이다.
DSB-SC의 경우 SNRc=SNRo이므로, 각각
a. 입력 SNR=10dB
b. 입력 SNR=0dB
b. 입력 SNR=-10dB
2) FM


a. 입력 SNR=10dB
b. 입력 SNR=-10dB
입력SNR(dB)
+10dB
0dB
-10dB
AM
SNRo
SNRc
가치지수
1
1
1
FM
SNRo
SNRc
가치지수
0.00882
0.00882
3) Mean Square Error
-10dB
0dB
10dB
AM
0.0445
0.0442
0.0421
분석: 일정하게 입력되는 음성신호와 그 power에 대해서 입력 SNR이 작아질수록 No값이 증가한다. 이것은 [표1]에서 확인할 수 있듯이 출력 SNR과 채널 SNR값에 영향을 미치며, 궁극적으로 가치지수(figure of merit)을 결정한다. SNR이 높을수록 가치지수가 높고 이는 더 나은 Modulation scheme이라는 것을 알 수 있다.
또한, [표2]의 AM의 MSE 시뮬레이션 결과를 보자. 입력 SNR이 커질수록 MSE는 작아진다는 것을 알 수 있다. 여기서 MSE란 message signal(우리팀의 음성파일 s1.wav)과 변복조되어 나온 결과 signal의 차이를 제곱하여 평균을 구한 값이다.
수치적 결과들을 귀로도 확인 할 수 있습니다. AM은 -10dB의 SNR을 입력으로 주었을 때, FM은 10dB 보다는 -10dB 일 때 확실히 음질이 더 떨어진다는 것을 확인했다.
한 가지 아쉬운 점은, 음원을 선택했을 때 threshold effect를 확인해야 한다는 것을 간과하고 클릭 소리를 이미 배경으로 한 것을 선택해 버렸다. 이것은 이 효과를 귀로 확인 하는데 있어 어려움으로 작용했다.

키워드

matlab,   FM,   AM,   변조기 ,   복조기