◎ 안정도 판별

목차

◎ 안정도 판별

◎ 선형 비선형 모든 미분방정식 풀수 있는 방법:Runge-kutta법

◎ 2계 미분 방정식(R-L-C시스템)

본문내용

◎ 안정도 판별
모든 시스템은 미방으로 표현 가능 하다
◎ 선형 비선형 모든 미분방정식 풀수 있는 방법:Runge-kutta법
Rk법 이용 미분방정식 푸는 함수 : ode45
ode45(@함수명, 시작 종료 , 초기값)
*@함수명=미방
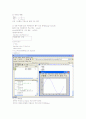
function xdot=kky(t,x)
미분방정식 구현
ex)x=cos(t)
x→sin
function xdot = kky(t,x)
xdot=cos(t);
>>[t,x]=ode45(@kky,[0 2*pi],0)
>>plot(t,x)
*[t,x]→리턴값
함수는 무조건 m-file로 저장 되어야 한다.
함수의 이름과 동일한 이름으로 저장 되어야 한다(kky)
◎ 2계 미분 방정식(R-L-C시스템)
spring-damper system
F(t)=M*(t)+B*(t)+K*x(t)
M*(t) : 관성력, 변위→2계 미분→가속도
B*(t) : 마찰력, 댐퍼, 속도↑-마찰력↑, 변위→미분→속도, 속도에 관련
K*x(t) : 스프링 상수(탄성계수)
*n개 미방 → n개의 1계 미방으로 바꿀 수 있다.
2계 미방 → 2개의 1계 미방
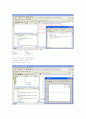
function xdot=springdamper(t,x)
x1dot=x(2);
x2dot=
xdot=[x1dot ; x2dot];
M*(t)=F(t)-B*(t)-K*x(t)
(t)=
2계미방
=Ax+Bu
[t,x]=ode45(@springdamper,[0 10],[0;0])
↓error(M,F,B,K 상수 정의 하지 않았기 때문)
function 과 xdot 사이에 global
command 창에도 똑같이 승인
B=2 , K=10 , F=0 , M=1
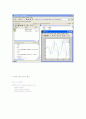
그래프가 생긴다. F가 0 초기값이 0이므로
x부분을 [10;0]으로 바꾼다.
legend('x1','x2')
ex)
ode45로 풀기
sol)
=-(x(1).^2-1)*x(2)-x(1);
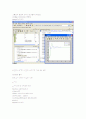
function xdot=van(t,x)
x1dot=x(2)
x2dot=-(x(1).^2-1*x(2)-x(1);
xdot=[x1dot ; x2dot]
[t,x]=ode45(@van,[0 20],[0;0.25]
plot(t,x)
legend('x1'.'x2')
*비선형 미분 방정식 풀이
1)
sol)function xdot=young(t,x)
x1dot=x(2);
x2dot=x(1)-sin(t);
xdot=[x1dot; x2dot];
2)
function xdot=young(t,x)
global c n
c = 10;
n = 5;
x1dot = 3*(x(1)+x(2)-(x(1)^3/3)-1.3);
x2dot = (c*x(1) - n*x(2)^2);
xdot=[x1dot;x2dot];

키워드

매트랩을 이용한 안정도 판별법