본문내용
bda=10\'); xlabel(\'x\'); ylabel(\'PDF of x\');
Problem 1. (c) MATLAB CODE λ = 10 & m = 1000
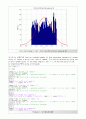
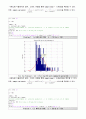
Plot the Problem 1. (c) : Plot the PDF with lambda=10 and m=1000
→ MATLAB 시뮬레이션 결과, 그래프 파형을 통해 sample mean = 0.09808임을 확인할 수 있다.
또한, sample variance는 을 확인할 수 있다.
clc; clear all
m = 1000;
lambda = 100;
x=-log(rand(1,m))./lambda;
% Create randexp(lambda, m) : generates exponential r.v. of length m, arrival rate of lambda
figure(1);
histfit(x, 50); % bin value is 50 and plot histogram
hold on
grid on
title(\'Plot the PDF with m=1000 & lambda=100\'); xlabel(\'x\'); ylabel(\'PDF of x\');
Problem 1. (c) MATLAB CODE λ = 100 & m = 1000
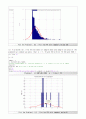
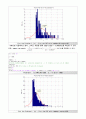
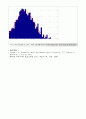
Plot the Problem 1. (c) : Plot the PDF with lambda=100 and m=1000
→ MATLAB 시뮬레이션 결과, 그래프 파형을 통해 sample mean = 0.009756임을 확인할 수 있다.
또한, sample variance는 을 확인할 수 있다.
2. Relationship of exponential and Gaussian distributions:
(a) Generate 1,000 samples whose PDF is normal (Gaussian) distribution N(10 25) using the MATLAB function randn().
→ MATLAB 시뮬레이션 과정 : MATLAB 함수 중 randn()함수와 histfit()함수를 사용.
help randn
RANDN Normally distributed random numbers.
R = RANDN(N) returns an N-by-N matrix containing pseudo-random values
drawn from a normal distribution with mean zero and standard deviation one.
RANDN(M,N) or RANDN([M,N]) returns an M-by-N matrix.
RANDN(M,N,P,...) or RANDN([M,N,P,...]) returns an M-by-N-by-P-by-... array.
RANDN with no arguments returns a scalar.
RANDN(SIZE(A)) returns an array the same size as A.
MATLAB 함수 : randn()함수 (MATLAB help)
clc; clear all
N = 10 + sqrt(25)*randn(1,1000); % Create normal(Gaussian) Distribution N(10,25)
histfit(N,50); % bin value is 50 and plot histogram
hold on
title(\'Plot the PDF with normal(Gaussian) Distribution N(10,25)\'); xlabel(\'N\'); ylabel(\'PDF of N\');
grid on
Problem 2. (a) MATLAB CODE
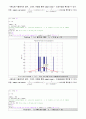
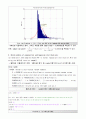
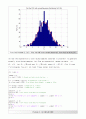
Plot the Problem 2. (a) : Plot the PDF with normal(Gaussian) Distribution N(10,25)
(b) Use the exponentially distributed samples obtained in problem 1 to generate normally distributed samples. Let R be an exponential random variable, i.e., . Let and , where Θ ~ U(0 2). Plot X\'s and Y\'s histogram. You will nd X and Y have normal distribution.
clc; clear all
lambda = 10;
U = rand (1,1000); % Create uniformly distribution r.v
E = -(1/lambda).*log(1-U); % Exponential distributed r.v
th = 2*pi*rand(1,1000); % uniformly distributed r.v range of 0~2pi
X = sqrt(E).*cos(th); % equation of X vector
Y = sqrt(E).*sin(th); % equation of Y vector
subplot(1, 2, 1);
histfit(X,50); % bin value is 50 and plot histogram
hold on
title(\'Plot the PDF of X with lambda=10\'); xlabel(\'X\'); ylabel(\'PDF of X\');
grid on
subplot(1, 2, 2);
histfit(Y,50); % bin value is 50 and plot histogram
hold on
title(\'Plot the PDF of Y with lambda=10\'); xlabel(\'Y\'); ylabel(\'PDF of Y\');
grid on
Problem 2. (b) MATLAB CODE
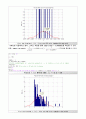
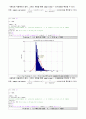
Plot the Problem 2. (b) : Plot the PDF with normal(Gaussian) Distribution N(10,25)
< 참고문헌 >
- Probability, Random Variables and Random Signal Processing, P.Z. Peebles Jr.,
McGraw-Hill, 4th ed, 2001.
- MATLAB 객체 지향 프로그래밍 언어, 박전수 역, 아진, 2008.
Problem 1. (c) MATLAB CODE λ = 10 & m = 1000
Plot the Problem 1. (c) : Plot the PDF with lambda=10 and m=1000
→ MATLAB 시뮬레이션 결과, 그래프 파형을 통해 sample mean = 0.09808임을 확인할 수 있다.
또한, sample variance는 을 확인할 수 있다.
clc; clear all
m = 1000;
lambda = 100;
x=-log(rand(1,m))./lambda;
% Create randexp(lambda, m) : generates exponential r.v. of length m, arrival rate of lambda
figure(1);
histfit(x, 50); % bin value is 50 and plot histogram
hold on
grid on
title(\'Plot the PDF with m=1000 & lambda=100\'); xlabel(\'x\'); ylabel(\'PDF of x\');
Problem 1. (c) MATLAB CODE λ = 100 & m = 1000
Plot the Problem 1. (c) : Plot the PDF with lambda=100 and m=1000
→ MATLAB 시뮬레이션 결과, 그래프 파형을 통해 sample mean = 0.009756임을 확인할 수 있다.
또한, sample variance는 을 확인할 수 있다.
2. Relationship of exponential and Gaussian distributions:
(a) Generate 1,000 samples whose PDF is normal (Gaussian) distribution N(10 25) using the MATLAB function randn().
→ MATLAB 시뮬레이션 과정 : MATLAB 함수 중 randn()함수와 histfit()함수를 사용.
help randn
RANDN Normally distributed random numbers.
R = RANDN(N) returns an N-by-N matrix containing pseudo-random values
drawn from a normal distribution with mean zero and standard deviation one.
RANDN(M,N) or RANDN([M,N]) returns an M-by-N matrix.
RANDN(M,N,P,...) or RANDN([M,N,P,...]) returns an M-by-N-by-P-by-... array.
RANDN with no arguments returns a scalar.
RANDN(SIZE(A)) returns an array the same size as A.
MATLAB 함수 : randn()함수 (MATLAB help)
clc; clear all
N = 10 + sqrt(25)*randn(1,1000); % Create normal(Gaussian) Distribution N(10,25)
histfit(N,50); % bin value is 50 and plot histogram
hold on
title(\'Plot the PDF with normal(Gaussian) Distribution N(10,25)\'); xlabel(\'N\'); ylabel(\'PDF of N\');
grid on
Problem 2. (a) MATLAB CODE
Plot the Problem 2. (a) : Plot the PDF with normal(Gaussian) Distribution N(10,25)
(b) Use the exponentially distributed samples obtained in problem 1 to generate normally distributed samples. Let R be an exponential random variable, i.e., . Let and , where Θ ~ U(0 2). Plot X\'s and Y\'s histogram. You will nd X and Y have normal distribution.
clc; clear all
lambda = 10;
U = rand (1,1000); % Create uniformly distribution r.v
E = -(1/lambda).*log(1-U); % Exponential distributed r.v
th = 2*pi*rand(1,1000); % uniformly distributed r.v range of 0~2pi
X = sqrt(E).*cos(th); % equation of X vector
Y = sqrt(E).*sin(th); % equation of Y vector
subplot(1, 2, 1);
histfit(X,50); % bin value is 50 and plot histogram
hold on
title(\'Plot the PDF of X with lambda=10\'); xlabel(\'X\'); ylabel(\'PDF of X\');
grid on
subplot(1, 2, 2);
histfit(Y,50); % bin value is 50 and plot histogram
hold on
title(\'Plot the PDF of Y with lambda=10\'); xlabel(\'Y\'); ylabel(\'PDF of Y\');
grid on
Problem 2. (b) MATLAB CODE
Plot the Problem 2. (b) : Plot the PDF with normal(Gaussian) Distribution N(10,25)
< 참고문헌 >
- Probability, Random Variables and Random Signal Processing, P.Z. Peebles Jr.,
McGraw-Hill, 4th ed, 2001.
- MATLAB 객체 지향 프로그래밍 언어, 박전수 역, 아진, 2008.






















소개글