목차
1. Simulate the experiment of a coin toss with P(head) = p as follows:
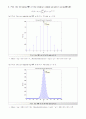
2. Plot the following PMF of the binomial random variable X using MATLAB:
3. The De Moivre-Laplace theorem is an approximation of the binomial distribution to a normal distribution, i.e.
< 참고문헌 >
2. Plot the following PMF of the binomial random variable X using MATLAB:
3. The De Moivre-Laplace theorem is an approximation of the binomial distribution to a normal distribution, i.e.
< 참고문헌 >
본문내용
0 and p=0.5\'); xlabel(\'N\'); ylabel(\'P(X=k)\');
n = 100; % Problem 2.(b)
p = 0.5;
k = 0:n;
y = binopdf(k, n, p);
subplot(2, 2, 2);
stem(k, y);
hold on
title(\'Plot the PMF with N=100 and p=0.5\'); xlabel(\'N\'); ylabel(\'P(X=k)\');
n = 10; % Problem 2.(c)
p = 0.3;
k = 0:n;
y = binopdf(k, n, p);
subplot(2, 2, 3);
stem(k, y);
hold on
title(\'Plot the PMF with N=10 and p=0.3\'); xlabel(\'N\'); ylabel(\'P(X=k)\');
n = 100; % Problem 2.(d)
p = 0.3;
k = 0:n;
y = binopdf(k, n, p);
subplot(2, 2, 4);
stem(k, y);
hold on
title(\'Plot the PMF with N=100 and p=0.3\'); xlabel(\'N\'); ylabel(\'P(X=k)\');
Problem 2. (a) ~ (d) MATLAB CODE
3. The De Moivre-Laplace theorem is an approximation of the binomial
distribution to a normal distribution, i.e.,
Here, q = 1 p.
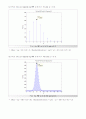
(a) Plot the PMF of binomial random variable with (N; p) = (200 0:3).
Plot the PMF of binonial random variable with N=200 and p=0.3
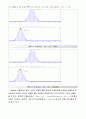
(b) Plot the PDF of its corresponding normal distribution N(Np;Npq).
Plot the PMF of normal distriution(mean = np, variance = npq)
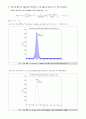
(c) Compare the two gures and discuss the central limit theorem.
Compare Plot the PMF of binonial random variable & Plot the PMF of normal distriution
→ MATLAB 시뮬레이션 결과, (a) PMF(확률질량함수)와 (b) PDF(확률밀도함수)의 그래프 모양은 거의 일치함을 알 수 있었다. 그러나 (a) PMF는 이산확률변수 X의 분포를 함수로 나타낸 것으로 Discrete하며, (b) PDF는 연속확률변수 X의 확률상황 분포를 곡선(직선)으로 나타낸 것으로 Continuous하다. 따라서 (a) PMF와 (b) PDF는 그래프 모양은 거의 일치하지만 Discrete와 Continuous의 차이점을 갖고 있다.
(d) Discuss the relationship of the experimental results of problem 1 and the cental limit theorem.
→ central limit theorem은 확률변수 제n항까지의 합의 분포가 n → ∞일 때 정규분포에 가까워지는 것을 보이는 정리이다. 즉, X를 이항분포 nCkpkqn-k(p는 바라는 사건이 일어날 확률, q=1-p)에 따르는 확률변수라 하면, (np는 X의 평균값, √npq는 X의 표준편차)의 분포는 n → ∞일 때 표준정규분포 N(0,1)에 가까워진다. 일반적으로, 이항분포에 따르는 확률변수X는 값 0, 1만을 취하는 독립인 확률변수의 합으로서 표시된다. 앞의 식은 이와 같은 변수에 관한 서술이지만, 서로 다른 분포에 따르는 독립인 확률변수의 열에 대해서도 중심극한정리는 성립한다. 즉, X1, X2, … Xn은 서로 독립이며, 평균값 E(Xj=mj, 분산 V(Xj)=σj2(j=1, 2, …)을 가지는 것으로 한다. 그때 어떤 조건하에서 n을 충분히 크게 하면, 은 근사적으로 정규분포 N(0, 1)에 따라 분포한다.
따라서, 문제1의 반복적인 실험에 의해 측정된 PMF와 이항 분포, De Moivre-Laplace approximation, 가우시안 분포에 대해서 살펴보면
. 즉, PMF를 통해서 가우시안 분포로 근접할 수 있다. 하지만 반대로 가우시안을 PMF로 나타낼 수 는 없다. 또한 PMF가 가우시안 분포로 접근하기는 하나 PMF는 결국 임펄스 파형이므로 완벽히 가우시안 분포와 같을 수 없다. X를 이항분포 에 따르는 PMF 함수의 평균은 , 분산은 를 가지게 되며, 가우시안 분포로 표현을 해보면 , 이고, PMF와 같은 평균, 분산값을 가질 것 이므로 으로 나타 낼 수 있다. 따라서 PMF가 가우시안 분포에 거의 근접한다는 것을 알 수 있다.
clc; clear all
n = 200; % Problem 3.(a)
k = 0:n;
p = 0.3;
q = 1-p;
y = binopdf(k, n, p);
subplot(1, 2, 1)
plot(k, y)
xlim([0 n])
stem(k, y);
hold on
title(\'Plot the PMF of binonial random variable with N=200 and p=0.3\'); xlabel(\'N\'); ylabel(\'P(X=k)\');
y = pdf(\'Normal\',0:n, n*p, sqrt(n*p*q)); % Problem 3.(b)
subplot(1, 2, 2)
plot(k, y);
xlim([0 n])
hold on
title(\'Plot the PMF of normal distriution(mean = np, variance = npq)\'); xlabel(\'N\'); ylabel(\'P(X=k)\');
Problem 3. (a) ~ (b) MATLAB CODE
< 참고문헌 >
- Probability, Random Variables and Random Signal Processing, P.Z. Peebles Jr.,
McGraw-Hill, 4th ed, 2001.
- MATLAB 객체 지향 프로그래밍 언어, 박전수 역, 아진, 2008.
n = 100; % Problem 2.(b)
p = 0.5;
k = 0:n;
y = binopdf(k, n, p);
subplot(2, 2, 2);
stem(k, y);
hold on
title(\'Plot the PMF with N=100 and p=0.5\'); xlabel(\'N\'); ylabel(\'P(X=k)\');
n = 10; % Problem 2.(c)
p = 0.3;
k = 0:n;
y = binopdf(k, n, p);
subplot(2, 2, 3);
stem(k, y);
hold on
title(\'Plot the PMF with N=10 and p=0.3\'); xlabel(\'N\'); ylabel(\'P(X=k)\');
n = 100; % Problem 2.(d)
p = 0.3;
k = 0:n;
y = binopdf(k, n, p);
subplot(2, 2, 4);
stem(k, y);
hold on
title(\'Plot the PMF with N=100 and p=0.3\'); xlabel(\'N\'); ylabel(\'P(X=k)\');
Problem 2. (a) ~ (d) MATLAB CODE
3. The De Moivre-Laplace theorem is an approximation of the binomial
distribution to a normal distribution, i.e.,
Here, q = 1 p.
(a) Plot the PMF of binomial random variable with (N; p) = (200 0:3).
Plot the PMF of binonial random variable with N=200 and p=0.3
(b) Plot the PDF of its corresponding normal distribution N(Np;Npq).
Plot the PMF of normal distriution(mean = np, variance = npq)
(c) Compare the two gures and discuss the central limit theorem.
Compare Plot the PMF of binonial random variable & Plot the PMF of normal distriution
→ MATLAB 시뮬레이션 결과, (a) PMF(확률질량함수)와 (b) PDF(확률밀도함수)의 그래프 모양은 거의 일치함을 알 수 있었다. 그러나 (a) PMF는 이산확률변수 X의 분포를 함수로 나타낸 것으로 Discrete하며, (b) PDF는 연속확률변수 X의 확률상황 분포를 곡선(직선)으로 나타낸 것으로 Continuous하다. 따라서 (a) PMF와 (b) PDF는 그래프 모양은 거의 일치하지만 Discrete와 Continuous의 차이점을 갖고 있다.
(d) Discuss the relationship of the experimental results of problem 1 and the cental limit theorem.
→ central limit theorem은 확률변수 제n항까지의 합의 분포가 n → ∞일 때 정규분포에 가까워지는 것을 보이는 정리이다. 즉, X를 이항분포 nCkpkqn-k(p는 바라는 사건이 일어날 확률, q=1-p)에 따르는 확률변수라 하면, (np는 X의 평균값, √npq는 X의 표준편차)의 분포는 n → ∞일 때 표준정규분포 N(0,1)에 가까워진다. 일반적으로, 이항분포에 따르는 확률변수X는 값 0, 1만을 취하는 독립인 확률변수의 합으로서 표시된다. 앞의 식은 이와 같은 변수에 관한 서술이지만, 서로 다른 분포에 따르는 독립인 확률변수의 열에 대해서도 중심극한정리는 성립한다. 즉, X1, X2, … Xn은 서로 독립이며, 평균값 E(Xj=mj, 분산 V(Xj)=σj2(j=1, 2, …)을 가지는 것으로 한다. 그때 어떤 조건하에서 n을 충분히 크게 하면, 은 근사적으로 정규분포 N(0, 1)에 따라 분포한다.
따라서, 문제1의 반복적인 실험에 의해 측정된 PMF와 이항 분포, De Moivre-Laplace approximation, 가우시안 분포에 대해서 살펴보면
. 즉, PMF를 통해서 가우시안 분포로 근접할 수 있다. 하지만 반대로 가우시안을 PMF로 나타낼 수 는 없다. 또한 PMF가 가우시안 분포로 접근하기는 하나 PMF는 결국 임펄스 파형이므로 완벽히 가우시안 분포와 같을 수 없다. X를 이항분포 에 따르는 PMF 함수의 평균은 , 분산은 를 가지게 되며, 가우시안 분포로 표현을 해보면 , 이고, PMF와 같은 평균, 분산값을 가질 것 이므로 으로 나타 낼 수 있다. 따라서 PMF가 가우시안 분포에 거의 근접한다는 것을 알 수 있다.
clc; clear all
n = 200; % Problem 3.(a)
k = 0:n;
p = 0.3;
q = 1-p;
y = binopdf(k, n, p);
subplot(1, 2, 1)
plot(k, y)
xlim([0 n])
stem(k, y);
hold on
title(\'Plot the PMF of binonial random variable with N=200 and p=0.3\'); xlabel(\'N\'); ylabel(\'P(X=k)\');
y = pdf(\'Normal\',0:n, n*p, sqrt(n*p*q)); % Problem 3.(b)
subplot(1, 2, 2)
plot(k, y);
xlim([0 n])
hold on
title(\'Plot the PMF of normal distriution(mean = np, variance = npq)\'); xlabel(\'N\'); ylabel(\'P(X=k)\');
Problem 3. (a) ~ (b) MATLAB CODE
< 참고문헌 >
- Probability, Random Variables and Random Signal Processing, P.Z. Peebles Jr.,
McGraw-Hill, 4th ed, 2001.
- MATLAB 객체 지향 프로그래밍 언어, 박전수 역, 아진, 2008.



























소개글