시계열분석입문 - 담배값에 대한 시계열 분석

소개글

시계열분석입문 - 담배값에 대한 시계열 분석에 대한 보고서 자료입니다.

목차

Ⅰ주제선정

Ⅱ데이터수집

Ⅲ회귀모형추정

Ⅳ추정된 모형 검정
1. 적합성 검정
2. 회귀계수 검정
3. Durbin Watson - Test
4. Run Test

Ⅴ시계열 자료의 예측
1. Moving Average
2. Simple Exponential Smoothing
3. Forecasting with the Holt - Winters Method (in nonseasonal series)

Ⅵ. 느낀점

본문내용

D ERROR가 발생하므로 추정된 회귀모형이 오차항의 영향을 받으므로 회귀모형의 수정을 가하여야 한다. 이때 사용되는 귀무가설의 검정방법은 다음과 같다.
DURBIN WATSON 통계량 d = 과 같이 정의된다.
d=1.194
Durbin-Watson test statistic TABLE에서
1) n=24, K=2, α(유의수준) = 0.05
d = 1.19 , d = 1.55
2) n=24, K=2, α(유의수준) = 0.01
d = 0.96 , d = 1.30
귀무가설의 기각역인 (dd)에도 속하지 않으므로 자기상관이 있는지 없는지 알 수 없다.
4. Run Test
H : The series is random
중앙값 = 1958.5
자료는(--++++++++-+++-+--------)이므로
R=7, n=24
Z = = -2.5 이다.
이 때, Zα = - 2.5 이면 α = 0.0062 (0.62%) 이다. 0.62%가 랜덤하다고 나타나며, 0.62%보다 크면 랜덤하지 않게 된다. 유의수준 5% 하에서 이것을 본다면, 귀무가설 H는 기각된다. 그러므로 이 자료는 랜덤하지 않다는 결론이 나온다.
Ⅴ.시계열 자료의 예측
1. Moving Average
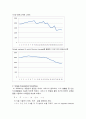
이동 평균법을 통해서 불규칙 요소들의 영향을 줄이고, 그래프를 보다 매끄럽게 만들어 준다. 먼저 simple centered 5-point Moving Average를 이용해 보았다.
X =
1인당 담배소비량 그래프
Simple centered 5-point Moving Average를 활용한 1인당 연간 담배소비량
2. Simple Exponential Smoothing
이 자료에서는 계절성과 일정한 추세가 나타나지 않으므로, 지수 평활법 중 단순지수평활법을 사용해 보도록 하겠다. 그리고 이 방법을 통해 과거와 현재의 관측값들을 사용하여 미래값을 예상해 보겠다.
_ _
X = X + (1 -)X (0 < < 1)
이 식을 사용하기 전에, 먼저 값을 정해줘야 한다.
= 0.1, 0.2, 0.3, 0.4을 각 각 넣어서 e를 구하고, sum of squared forecast errors를 구해보았다.
e =
= 0.1 일 때, SS = 567764
= 0.2 일 때, SS = 556706
= 0.3 일 때, SS = 559992
= 0.4 일 때, SS = 582309
= 0.2 일 때 가장 작은 값을 갖는다.
_ _
그로 인해, X = 0.2X + 0.8X 라는 식이 만들어졌다.
2009년 이후로는 1인당 연간 담배소비량으로 1294개비를 예상할 수 있다.
3. Forecasting with the Holt - Winters Method (in nonseasonal series)
이와 같이 계절성이 없는 자료의 경우에도 Holt-Winters 방법으로 예측이 가능하다. 예측방법은 다음과 같다.
먼저, 다음과 같이 기초값을 설정한다.
_
X = X , T = X - X
_ _
그리고 X = A( X + T ) + (1-A)X , ( 0 _ _
T = BT + (1-B)( X - X ) , ( 0 이 식에 따라 각 레벨을 대표하는 추정값과 트렌드의 추정값을 구한다.
A=0.3, B=0.4 로 일정한 값을 임의로 지정하였다.
_ _
X = 0.3( X + T ) + 0.7X
_ _
T = 0.4T + 0.6( X - X )
+ hT ( h= 1, 2, 3, ... ) 에 의해 미래 값을 예측할 수 있다.
2009년도 예측값은 1269 + 1*(-18) = 1251
2010년도 예측값은 1269 + 2*(-18) = 1233
2011년도 예측값은 1269 + 3*(-18) = 1215
이후로도 위와 같은 방법으로 예측을 한다.
Ⅵ. 느낀점
마지막으로 과제를 하면서 지금까지 수업을 하면서 배웠던 내용을 활용할 수 있었습니다. 개인적으로 담배값 인상에 따른 흡연율분석을 다른 수업을 통해 했었는데 그때는 시계열을 이용해서 하지 않아 문제가 많았습니다. 이번 과제 또한 완벽하게 수행했다고 자신할 수는 없지만 시계열 자료분석이라는 개념을 어느 정도 이해할 수 있게 되었습니다. 수업시간에 나름대로 잘 들으려고 노력했는데 부족한 점이 있었는지 분석할 때 어려움을 겪었습니다. 이 수업을 통해서 자료분석에 대해 많이 배웠습니다. 한 학기동안 가르쳐 주셔서 감사했습니다.

키워드

담배값에 대한 시계열 분석,   시계열분석입문,   시계열분석입문 - 담배값에 대한 시계열 분석,   시계열 자료의 예측,   회귀모형추정,   데이터수집