목차
제 1절 표본조사와 전수조사
제 2절 표본설계과정
제 2절 표본설계과정
본문내용
보니 가장 나이 많은 사람이 32살이고 가장 나이 어린 사람이
20살이었다. 그러므로 최대값과 최소값의 차이는 12이며 이를 6으로 나누어 보면
σ는 2가 된다. 또한 허용 가능한 표본평균과 모집단평균 차이(E)를 1.0 이라고 하자.
따라서 신뢰수준을 95%로 하면 Z 값은 1.96이다.
즉, n = ==24.5
그러므로 필요한 표본의 수는 16개가 된다.
(2)가설검증접근법
기본적인 논리는 신뢰구간접근법과 동일하나 이 접근법은 Type I 오차와 Type II
오차의 최대허용치를 정하고, 이를 통하여 표본의 수를 결정하는 방법이다. 그 절차는
다음과 같다.
①귀무가설과 대체가설의 수치를 정한다.
앞의 예의 경우를 들어보자. 50명의 나이를 추정한 것은 입사제도를 바꾼 뒤의
측정이었다고 하고, 이전까지 신입사원들의 나이는 평균 25살이었다고 하자. 그러나
입사제도 변경으로 입사시험이 어려워져서 2번 또는 3번 응시자들이 많아지고
경력사원이 늘어남에 따라 평균 29살이 되면 입사제도의 변경이 효과가 있는 것으로
간주하기로 하였다. 그러므로 귀무가설(H0)은 \"신입사원들의 나이가 25살이다\"이고,
대체가설(H1)은 \"신입사원들의 나이가 29살이 다\"가 된다.
②Type I 오차와 Type II 오차가 일어날 확률을 정한다.
α위험(type I)이 일어날 확률은 귀무가설이 맞으나 이를 틀리다고 할 확률이고,
β위험(type II)은 귀무가설이 틀리나 맞다고 할 확률이다.
본 예에서는 α위험을 0.05, β위험을 0.01로 하자.
③α위험과 β위험에 따른 Z 값(standard error)을 정한다.
α위험이 0.05일 때 β값은 1.64
α위험이 0.01일 때 β값은 2.33이 된다.
④모집단의 표본오차( α)를 추정한다.
앞의 신뢰구간접근법과 동일하다. 본 예에서는 3살로 추정하였다.
⑤표본크기의 결정
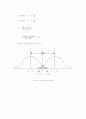
다음의 [그림 6-4]에서 보면 평균이 μ0, μ1 인 정규분포를 이루는 두 표본분포에서
각각 허용된 α위험, β위험의 수준을 모두 만족시키는 점은 동일하여야 한다. 그림에서
평균이 μ0 인 정규분포는 귀무가설이 맞다고 가정할 때의 분포이며, 평균이 μ1 인
정규분포는 대체가설이 맞다고 가정할 때의 분포이다. 그러므로 이를 표시하는 식은
다음과 같다.
μ0 분포에서 μ0 + Zα
μ1 분포에서 μ1 + Zβ
n=
= =8.87
그러므로 필요 표본수는 9개가 된다.
[그림 10-5] 표본크기의 결정
20살이었다. 그러므로 최대값과 최소값의 차이는 12이며 이를 6으로 나누어 보면
σ는 2가 된다. 또한 허용 가능한 표본평균과 모집단평균 차이(E)를 1.0 이라고 하자.
따라서 신뢰수준을 95%로 하면 Z 값은 1.96이다.
즉, n = ==24.5
그러므로 필요한 표본의 수는 16개가 된다.
(2)가설검증접근법
기본적인 논리는 신뢰구간접근법과 동일하나 이 접근법은 Type I 오차와 Type II
오차의 최대허용치를 정하고, 이를 통하여 표본의 수를 결정하는 방법이다. 그 절차는
다음과 같다.
①귀무가설과 대체가설의 수치를 정한다.
앞의 예의 경우를 들어보자. 50명의 나이를 추정한 것은 입사제도를 바꾼 뒤의
측정이었다고 하고, 이전까지 신입사원들의 나이는 평균 25살이었다고 하자. 그러나
입사제도 변경으로 입사시험이 어려워져서 2번 또는 3번 응시자들이 많아지고
경력사원이 늘어남에 따라 평균 29살이 되면 입사제도의 변경이 효과가 있는 것으로
간주하기로 하였다. 그러므로 귀무가설(H0)은 \"신입사원들의 나이가 25살이다\"이고,
대체가설(H1)은 \"신입사원들의 나이가 29살이 다\"가 된다.
②Type I 오차와 Type II 오차가 일어날 확률을 정한다.
α위험(type I)이 일어날 확률은 귀무가설이 맞으나 이를 틀리다고 할 확률이고,
β위험(type II)은 귀무가설이 틀리나 맞다고 할 확률이다.
본 예에서는 α위험을 0.05, β위험을 0.01로 하자.
③α위험과 β위험에 따른 Z 값(standard error)을 정한다.
α위험이 0.05일 때 β값은 1.64
α위험이 0.01일 때 β값은 2.33이 된다.
④모집단의 표본오차( α)를 추정한다.
앞의 신뢰구간접근법과 동일하다. 본 예에서는 3살로 추정하였다.
⑤표본크기의 결정
다음의 [그림 6-4]에서 보면 평균이 μ0, μ1 인 정규분포를 이루는 두 표본분포에서
각각 허용된 α위험, β위험의 수준을 모두 만족시키는 점은 동일하여야 한다. 그림에서
평균이 μ0 인 정규분포는 귀무가설이 맞다고 가정할 때의 분포이며, 평균이 μ1 인
정규분포는 대체가설이 맞다고 가정할 때의 분포이다. 그러므로 이를 표시하는 식은
다음과 같다.
μ0 분포에서 μ0 + Zα
μ1 분포에서 μ1 + Zβ
n=
= =8.87
그러므로 필요 표본수는 9개가 된다.
[그림 10-5] 표본크기의 결정
키워드
추천자료
 조사설계평가보고서
조사설계평가보고서 단일 사례 조사설계
단일 사례 조사설계 사회과학 조사설계서
사회과학 조사설계서 [사회과학] 실험조사설계의 기본요건과 유형(전실험조사설계, 유사실험조사설계, 순수실험조...
[사회과학] 실험조사설계의 기본요건과 유형(전실험조사설계, 유사실험조사설계, 순수실험조... 실험조사설계의 기본요건과 유형(전실험조사설계, 유사실험조사설계, 순수실험조사설계)
실험조사설계의 기본요건과 유형(전실험조사설계, 유사실험조사설계, 순수실험조사설계) [사회복지조사론] 연구주제를 개인별로 정하여 연구설계를 직접제출
[사회복지조사론] 연구주제를 개인별로 정하여 연구설계를 직접제출 실험조사설계의 기본요건과 유형(전실험조사설계, 유사실험조사설계,순수실험조사설계)에 대...
실험조사설계의 기본요건과 유형(전실험조사설계, 유사실험조사설계,순수실험조사설계)에 대... [여론조사][여론조사 종류][여론조사 조사설계][커뮤니케이션]여론조사의 의의, 여론조사의 ...
[여론조사][여론조사 종류][여론조사 조사설계][커뮤니케이션]여론조사의 의의, 여론조사의 ... 조사연구 설계시 타당도와 신뢰도 확보는 가장 중요한 요인들이다. 타당도와 신뢰도가 무엇인...
조사연구 설계시 타당도와 신뢰도 확보는 가장 중요한 요인들이다. 타당도와 신뢰도가 무엇인... 사회복지조사론_사회복지조사를 통해 나온 실제 이론 한가지를 학술연구지에서 찾아 선택하여...
사회복지조사론_사회복지조사를 통해 나온 실제 이론 한가지를 학술연구지에서 찾아 선택하여... [사회복지조사론] 단일체계설계를 활용한 부적절한 섭식행동을 보이는 (만) 6세 유아에 대한 ...
[사회복지조사론] 단일체계설계를 활용한 부적절한 섭식행동을 보이는 (만) 6세 유아에 대한 ... [사회복지조사론 단일체계설계] 사회복귀시설의 직업재활 서비스가 정신장애인의 삶의 질 만...
[사회복지조사론 단일체계설계] 사회복귀시설의 직업재활 서비스가 정신장애인의 삶의 질 만... 사회복지조사론 ) 본인이 관심을 갖고 있는 사회문제에 대한 조사 설계 시 가장 적절한 표집...
사회복지조사론 ) 본인이 관심을 갖고 있는 사회문제에 대한 조사 설계 시 가장 적절한 표집...


























소개글