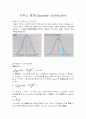
|
있으며, 이 인자를 볼츠만인자(因子)라고 한다. 단, 이들 법칙은 기체의 퇴화(退化)를 무시할 수 없을 때는 수정이 필요하다. - 가우스 분포(Gaussian Distribution)
- 이항분포(Binomial Distribution)
- 맥스웰 볼츠만 분포(Maxwell Boltzman Distribution)
|
|
|
가우스의 법칙
22. 전기퍼텐셜
23. 축전기와 전기용량
24. 전류와 저항
25. 회로 이론
26. 자기장
27. 전자기적 진동과 교류
28. 맥스웰 방정식, 물질의 자성
29. 전자기파
30. 빛의 반사와 굴절 그리고 간섭, 회절
31. Einstein의 상대론
32. 광자와
|
|
|
분포
-[네이버 지식백과] 이산확률분포
-[네이버 지식백과] 연속확률분포
-[네이버 지식백과] 이항분포
-[네이버 지식백과] 정규분포
-[네이버 지식백과] 포아송분포
-[네이버 지식백과] 초기하분포
-[네이버 지식백과] 가우스분포
-[네이버 지식
|
|
|
맥스웰-볼츠만 분포의 개념을 금융시장에 어떻게 적용할 수 있는지 설명하고,
이를 통해 시장 참여자의 심리 상태를 분석하며,
온도(거래량, 변동성)의 높고 낮음에 따라 적절한 매매전략이 어떻게 달라지는지 구체적으로 제시하는 것입니
|
|
|
분포형으로 정규분포가 연속변량인 데 대하여 이항분포는 이산변량이다. 이항분포를 B(n,p)로 나타낼 때 평균값 m은 m＝np, 분산 σ2은 σ2=npq(q=1－p)임이 증명되어 있으며 p가 0이나 1에 가깝지 않고 n이 충분히 크면 이항분포는 정규분포(가우스분
|
|
 |
이항분포 ․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․․R
|
|
 |
분포에 대하여 설명해보세요.
32
msds란 무엇인가요?
33
기존 직장에서 가장 잘못했던 사례와 해결책은 무엇인가요?
34
맥스웰 방정식에 대해 설명해보시오.
35
중대재해처벌법에 관한 자신의 견해를 말해주세요.
36
안전이 뭐라고 생각하는지?
37
|
|
메뉴펼치기
