|
우함수
(1) 우함수(짝함수) → 지수가 짝수인 함수
(x2, x4, ... 및 상수함수)
① 모든 x 에 대하여 f(-x)=f(x)
② 그래프는 y 축에 대하여 대칭
기함수
(2) 기함수(홀함수) → 지수가 홀수인 함수
(x, x3, x5, ...)
① 모든 x에 대하여
|
|
|
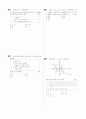
함수의 그래프
◈ 기본 그래프
① x축과 y축이 점근선이다
② (0, 0) 원점 대칭함수이다(기함수)
③ k > 0 이면 제 1, 3사분면을 지나고, k < 0 이면 제 2, 4사분면을 지난다
◈ 의 그래프
① 정의역은 , 치역은 이다.
② 점근선은
③ 점 에 대하
|
|
|
함수
◈ 의 그래프
① 의 그래프를 축, 축 방향으로 각각 만큼 평행이동한 것이다.
② 일 때 가 증가하면 도 증가하고, 일 때 가 증가하면 는 감소한다.
◈ 함수 에 대하여
① 우함수 : 축 대칭 짝수차 함수
② 기함수 : 원점 대칭 홀수 함수
9. 절
|
|
|
두 조건
(i)
(ii)
를 만족할 때, 를 구하는 풀이과정을 나타낸 것이다.
풀이 의 차수를 이라 하면 의 차수는 이고 의 차수는 이므로 또는 이다. 조건 (ii)에서 는 기함수이므로 이고
로 놓을 수 있다. 이 때, 조건 (i)에서
이 성립하고, 위의 식은
|
|
|
기함수
예 :
우함수
예 :
sin, cos
구형파, 삼각파
특성식
f(t) = - f(-t)
f(t) = f(-t)
f(t) = - f(t + )
특징
원점 대칭
y축 대칭
반주기 마다 파형이 교대로 +, - 값을 갖는다.
존재하는 항
sin항
cos항, 상수항
기수항(홀수항)
존재하지 않는 항
상수항, cos항
s
|
|
메뉴펼치기
