목차
1. 서론
2. 실험
3. 계산
4. 결론 및 고찰
5. 참고문헌
6. DATA SHEET
2. 실험
3. 계산
4. 결론 및 고찰
5. 참고문헌
6. DATA SHEET
본문내용
음과 같다.
식(4) :
이 식의 우변은 도식적분으로 다음과 같이 나타낼 수 있다.
③ 40wt% 에탄올 수용액 실험 결과표에서 에탄올의 조성인 은 39.63%이고, 위에서 계산한 유출률 는 0.5047이므로 이를 대입해 를 구할 수 있다.
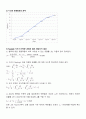
또한 는 Figure.3에서, 실험 결과로 나온 40wt% 에탄올의 조성인 =39.63%를 대입해 계산할 수 있다.
④ 이제 이론적인 방법으로 유출액의 평균조성을 구해보자. 유출량을 , 유출액의 조성을 라 하고 물질수지 식을 세우면 다음과 같다.
식(7) :
그러므로 유출액의 평균 조성의 이론적인 값은 다음과 같이 계산할 수 있다.
⑤ 그리고 비휘발도 와 유출률 의 다음 관계식을 이용해 비휘발도를 계산해보자.
→
⑥ 마지막으로 이번 실험의 결과값과 이론값을 비교해 오차율을 계산하고 다음 표에 정리하여 실험의 정확도를 판별해 보자. 여기에서 오차율을 계산하는 방법은 다음 식과 같다.
측정값
수용액
잔류액
유출액
40wt% 실험값
39.63
8.2690
72.2803
40wt% 이론값
39.63
12.00
66.75
오차율 (%)
-
31.09%
8.29%
4) 식(9)에 의한 잔액의 이론치를 구하고 실측치와 비교한다.
식(9) :
측정값
잔류액
40wt% 실험값
8.2690
40wt% 이론값
45.05
오차율 (%)
81.64%
<보고사항>
1) 시간과 온도와의 관계
2) 시간과 유출량과의 관계
3) Rayleigh 식의 도식적분 과정과 결과. 물질수지 결과
① 원료에 대한 유출액량의 비로 나타낼 수 있는 유출률 는 다음과 같이 정의된다.
② 그리고 Rayleigh 식을 이용해 유출률 에 대한 식으로 정리하면 다음과 같다.
식(4) :
이 식의 우변은 도식적분으로 다음과 같이 나타낼 수 있다.
③ 40wt% 에탄올 수용액 실험 결과표에서 에탄올의 조성인 은 39.63%이고, 위에서 계산한 유출률 는 0.5047이므로 이를 대입해 를 구할 수 있다.
또한 는 Figure.3에서, 실험 결과로 나온 40wt% 에탄올의 조성인 =39.63%를 대입해 계산할 수 있다.
④ 이제 이론적인 방법으로 유출액의 평균조성을 구해보자. 유출량을 , 유출액의 조성을 라 하고 물질수지 식을 세우면 다음과 같다.
식(7) :
그러므로 유출액의 평균 조성의 이론적인 값은 다음과 같이 계산할 수 있다.
⑤ 그리고 비휘발도 와 유출률 의 다음 관계식을 이용해 비휘발도를 계산해보자.
→
⑥ 마지막으로 이번 실험의 결과값과 이론값을 비교해 오차율을 계산하고 다음 표에 정리하여 실험의 정확도를 판별해 보자. 여기에서 오차율을 계산하는 방법은 다음 식과 같다.
측정값
수용액
잔류액
유출액
40wt% 실험값
39.63
8.2690
72.2803
40wt% 이론값
39.63
12.00
66.75
오차율 (%)
-
31.09%
8.29%
표1. 실험값과 이론값의 정리
<고찰>
결과 정리 후 나타난 위의 표1.을 보면 잔류액과 유출액에서 모두 31.09%와 8.29%의 오차가 발생한 것을 볼 수 있다. 특히 잔류액의 오차율을 보면 유출액과 달리 오차율이 매우 큰 것을 볼 수 있다. 그러므로 이렇게 실험의 결과가 정확하지 않게 나오게 된 원인을 분석해볼 필요가 있다고 생각해 다음과 같이 여러 오차의 원인들을 생각해보았다.
먼저 실험이 끝난 후, 단증류 실험 장치를 정리하는 과정에서 잔류액이 들어있는 비커에 물이 섞이게 하는 큰 실수를 하였다. (호스를 싱크대에서 분리하지 않고 실험대에서 분리해 버림) 결국 이 비커에 든 잔류액은 이후 실험과정과 계산과정에 포함하지 못했다. 그래서 결과 정리 후 나타난 위의 표1. 잔류액의 오차율을 보면 유출액과 달리 오차율이 매우 큰 것을 볼 수 있다. 이 점이 이번 실험에서 가장 아쉬운 점이다.
두번째는 단증류 실험 장치를 설치할 때 각 장치들을 연결해야 하기 때문에 연결 부위마다 유체가 빠져나가지 않도록 꼼꼼하게 밀봉시켜 주어야 했다. 이번 실험에서는 호일을 이용해 연결 부위를 밀봉했는데, 여기서 개인오차로 인한 열의 손실이 발생했음을 무시할 수 없다. 이로 인해 손실률의 계산에 변화가 생겼을 것이라고 생각한다.
세번째는 이번 실험에 사용한 여러 실험기구들에 남는 잔류 유체로 인한 오차도 있었을 것이라 생각한다. 단증류 실험은 유체의 양이 1g 만 손실되어도 실험의 오차율이 크게 달라지는 실험이다. 이번 실험에서는 밀도와 무게의 측정을 위해 비중병, 비커, 증류 플라스크와 삼각플라스크 등 여러 가지의 실험기구를 이용해 실험한다. 먼저 비커에서 수용액의 무게를 측정하고 그 수용액의 밀도를 계산하기 위해 비중병에 넣고, 다시 이 비중병의 수용액을 다시 플라스크에 옮겨 실험한다. 이렇게 유체가 여러 도구에 옮겨 담아지면서 플라스크에 옮겨지지 않고 남아있는 잔류 유체는 불가피하게 발생했을 것이고, 이러한 작은 무게의 변화로 인해 실험의 오차율에 영향을 주었을 것이라고 생각한다.
이번 실험은 40wt% 에탄올 수용액을 가열시켜 진행하는 단증류 실험이었다. 실험 후 잔류액과 유출액의 조성을 계산해 에탄올의 양을 측정하였고, 손실량을 계산하였다. Rayleigh 식을 이용해 결과값을 계산해 이를 실험값과 비교하여 오차율을 계산하였다. 이러한 정확도가 낮은 실험의 결과가 나온 원인을 분석해보고, 오차를 야기한 여러 가지 원인에 대해서 생각해보았다. 정확도가 더 높은 실험의 결과를 위한 방법은 유체가 흘러나가지 않도록 꼼꼼하고 정확하게 설치한 실험장치와 온도에 따라 변화하는 에탄올의 정확한 밀도의 값을 취해 주어야 한다는 것이다. 또한 순수한 에탄올을 얻기 위해서는 유출액을 다시 단증류해 실험을 반복해서 진행하는 것이다. 이렇게 하면 에탄올의 조성이 높아져 더 순수한 에탄올을 얻을 수 있을 것이다.
참고문헌
2) Warren L. McCabe 외 2인, “McCabe의 단위조작”, 7판, p.547~548, p.565~568, 사이플러스(2017)
3) 김학준, “화학공학개론”, p.102-108, 문운당(2000)
4) 박소진, “화학공학실험”, p.26-30, 충남대학교출판부(2010)
6. DATA SHEET
식(4) :
이 식의 우변은 도식적분으로 다음과 같이 나타낼 수 있다.
③ 40wt% 에탄올 수용액 실험 결과표에서 에탄올의 조성인 은 39.63%이고, 위에서 계산한 유출률 는 0.5047이므로 이를 대입해 를 구할 수 있다.
또한 는 Figure.3에서, 실험 결과로 나온 40wt% 에탄올의 조성인 =39.63%를 대입해 계산할 수 있다.
④ 이제 이론적인 방법으로 유출액의 평균조성을 구해보자. 유출량을 , 유출액의 조성을 라 하고 물질수지 식을 세우면 다음과 같다.
식(7) :
그러므로 유출액의 평균 조성의 이론적인 값은 다음과 같이 계산할 수 있다.
⑤ 그리고 비휘발도 와 유출률 의 다음 관계식을 이용해 비휘발도를 계산해보자.
→
⑥ 마지막으로 이번 실험의 결과값과 이론값을 비교해 오차율을 계산하고 다음 표에 정리하여 실험의 정확도를 판별해 보자. 여기에서 오차율을 계산하는 방법은 다음 식과 같다.
측정값
수용액
잔류액
유출액
40wt% 실험값
39.63
8.2690
72.2803
40wt% 이론값
39.63
12.00
66.75
오차율 (%)
-
31.09%
8.29%
4) 식(9)에 의한 잔액의 이론치를 구하고 실측치와 비교한다.
식(9) :
측정값
잔류액
40wt% 실험값
8.2690
40wt% 이론값
45.05
오차율 (%)
81.64%
<보고사항>
1) 시간과 온도와의 관계
2) 시간과 유출량과의 관계
3) Rayleigh 식의 도식적분 과정과 결과. 물질수지 결과
① 원료에 대한 유출액량의 비로 나타낼 수 있는 유출률 는 다음과 같이 정의된다.
② 그리고 Rayleigh 식을 이용해 유출률 에 대한 식으로 정리하면 다음과 같다.
식(4) :
이 식의 우변은 도식적분으로 다음과 같이 나타낼 수 있다.
③ 40wt% 에탄올 수용액 실험 결과표에서 에탄올의 조성인 은 39.63%이고, 위에서 계산한 유출률 는 0.5047이므로 이를 대입해 를 구할 수 있다.
또한 는 Figure.3에서, 실험 결과로 나온 40wt% 에탄올의 조성인 =39.63%를 대입해 계산할 수 있다.
④ 이제 이론적인 방법으로 유출액의 평균조성을 구해보자. 유출량을 , 유출액의 조성을 라 하고 물질수지 식을 세우면 다음과 같다.
식(7) :
그러므로 유출액의 평균 조성의 이론적인 값은 다음과 같이 계산할 수 있다.
⑤ 그리고 비휘발도 와 유출률 의 다음 관계식을 이용해 비휘발도를 계산해보자.
→
⑥ 마지막으로 이번 실험의 결과값과 이론값을 비교해 오차율을 계산하고 다음 표에 정리하여 실험의 정확도를 판별해 보자. 여기에서 오차율을 계산하는 방법은 다음 식과 같다.
측정값
수용액
잔류액
유출액
40wt% 실험값
39.63
8.2690
72.2803
40wt% 이론값
39.63
12.00
66.75
오차율 (%)
-
31.09%
8.29%
표1. 실험값과 이론값의 정리
<고찰>
결과 정리 후 나타난 위의 표1.을 보면 잔류액과 유출액에서 모두 31.09%와 8.29%의 오차가 발생한 것을 볼 수 있다. 특히 잔류액의 오차율을 보면 유출액과 달리 오차율이 매우 큰 것을 볼 수 있다. 그러므로 이렇게 실험의 결과가 정확하지 않게 나오게 된 원인을 분석해볼 필요가 있다고 생각해 다음과 같이 여러 오차의 원인들을 생각해보았다.
먼저 실험이 끝난 후, 단증류 실험 장치를 정리하는 과정에서 잔류액이 들어있는 비커에 물이 섞이게 하는 큰 실수를 하였다. (호스를 싱크대에서 분리하지 않고 실험대에서 분리해 버림) 결국 이 비커에 든 잔류액은 이후 실험과정과 계산과정에 포함하지 못했다. 그래서 결과 정리 후 나타난 위의 표1. 잔류액의 오차율을 보면 유출액과 달리 오차율이 매우 큰 것을 볼 수 있다. 이 점이 이번 실험에서 가장 아쉬운 점이다.
두번째는 단증류 실험 장치를 설치할 때 각 장치들을 연결해야 하기 때문에 연결 부위마다 유체가 빠져나가지 않도록 꼼꼼하게 밀봉시켜 주어야 했다. 이번 실험에서는 호일을 이용해 연결 부위를 밀봉했는데, 여기서 개인오차로 인한 열의 손실이 발생했음을 무시할 수 없다. 이로 인해 손실률의 계산에 변화가 생겼을 것이라고 생각한다.
세번째는 이번 실험에 사용한 여러 실험기구들에 남는 잔류 유체로 인한 오차도 있었을 것이라 생각한다. 단증류 실험은 유체의 양이 1g 만 손실되어도 실험의 오차율이 크게 달라지는 실험이다. 이번 실험에서는 밀도와 무게의 측정을 위해 비중병, 비커, 증류 플라스크와 삼각플라스크 등 여러 가지의 실험기구를 이용해 실험한다. 먼저 비커에서 수용액의 무게를 측정하고 그 수용액의 밀도를 계산하기 위해 비중병에 넣고, 다시 이 비중병의 수용액을 다시 플라스크에 옮겨 실험한다. 이렇게 유체가 여러 도구에 옮겨 담아지면서 플라스크에 옮겨지지 않고 남아있는 잔류 유체는 불가피하게 발생했을 것이고, 이러한 작은 무게의 변화로 인해 실험의 오차율에 영향을 주었을 것이라고 생각한다.
이번 실험은 40wt% 에탄올 수용액을 가열시켜 진행하는 단증류 실험이었다. 실험 후 잔류액과 유출액의 조성을 계산해 에탄올의 양을 측정하였고, 손실량을 계산하였다. Rayleigh 식을 이용해 결과값을 계산해 이를 실험값과 비교하여 오차율을 계산하였다. 이러한 정확도가 낮은 실험의 결과가 나온 원인을 분석해보고, 오차를 야기한 여러 가지 원인에 대해서 생각해보았다. 정확도가 더 높은 실험의 결과를 위한 방법은 유체가 흘러나가지 않도록 꼼꼼하고 정확하게 설치한 실험장치와 온도에 따라 변화하는 에탄올의 정확한 밀도의 값을 취해 주어야 한다는 것이다. 또한 순수한 에탄올을 얻기 위해서는 유출액을 다시 단증류해 실험을 반복해서 진행하는 것이다. 이렇게 하면 에탄올의 조성이 높아져 더 순수한 에탄올을 얻을 수 있을 것이다.
참고문헌
2) Warren L. McCabe 외 2인, “McCabe의 단위조작”, 7판, p.547~548, p.565~568, 사이플러스(2017)
3) 김학준, “화학공학개론”, p.102-108, 문운당(2000)
4) 박소진, “화학공학실험”, p.26-30, 충남대학교출판부(2010)
6. DATA SHEET
키워드
추천자료
 [화공 기초 실험] 단증류 (Simple Distillation) [결과] 실험결과
[화공 기초 실험] 단증류 (Simple Distillation) [결과] 실험결과 [화공 기초 실험] 단증류 [결과] - A+
[화공 기초 실험] 단증류 [결과] - A+ [화공 기초 실험] 단증류 - 과산화수소의 농도 측정 [결과]
[화공 기초 실험] 단증류 - 과산화수소의 농도 측정 [결과] [화공 기초 실험] 단증류 [결과] - 과정, 결과, 토의및 고찰
[화공 기초 실험] 단증류 [결과] - 과정, 결과, 토의및 고찰 [화공 기초 실험] 단증류 [결과] - 실험목적 및 방법, 관련이론 포함
[화공 기초 실험] 단증류 [결과] - 실험목적 및 방법, 관련이론 포함 [공학/컴퓨터/통신] [화공 기초 실험] 단증류 [예비+결과]
[공학/컴퓨터/통신] [화공 기초 실험] 단증류 [예비+결과] [화공 기초 실험] 단증류 [예비+결과]
[화공 기초 실험] 단증류 [예비+결과] 단증류 실험- 실험목적, 실험기구 및 시약, 주의사항, 이론,실험장치, 실험방법
단증류 실험- 실험목적, 실험기구 및 시약, 주의사항, 이론,실험장치, 실험방법 물과 메탄올의 기-액 평형 단증류 실험(그래프 그리기)
물과 메탄올의 기-액 평형 단증류 실험(그래프 그리기) 화학공학과 2학년 단증류실험 결과보고서
화학공학과 2학년 단증류실험 결과보고서



































소개글