목차
목차
1. 개요
2. 퍼지 제어의 특성
3. 퍼지 제어기 설계
4. 퍼지화
5. 규칙 베이스
6. 의사결정
7. 비퍼지화
1. 개요
2. 퍼지 제어의 특성
3. 퍼지 제어기 설계
4. 퍼지화
5. 규칙 베이스
6. 의사결정
7. 비퍼지화
본문내용
3 THEN u3 is U3
RN : IF eN is EN and
int`
eN is
int`
EN THEN uN is UN (식3)
식 (3)에서 E,
int`
E, U는 퍼지 변수이다. 그리고 제어 규칙의 전건부 e,
int`
e는 퍼지 제어기의 입력이며, 후건부의 u는 출력이다. 이때 i번째 제어규칙은 다음과 같다.
Ri = ( Ei
int`
Ei ) Ui (식4)
제어규칙들은 or 결합이기 때문에 n개의 제어규칙은 다음과 같다.
R = R1 R2 R3 ... RN =
BIGCUP from {{i}=1~} to n
Ri (식5)
입력을
E ^0 , INT E^0
라고 하면 출력
U^0
는 다음과 같다.
U^0 = R CIRC (E^0 TIMES INT E^0 )
##U^0 (u) = max[R(e, int e,u)`` BIGWEDGE `` E^0 (e) ``BIGWEDGE`` INT E^0 ( INT e)]
(식6)
여기서,
e^0 와 ~ TRIANGLE e^0
를 측정된 일반화된 수치라 하면 식 (6)에서
E^0
와
INT E^0
는 다음과 같다.
E^0 (e) ``=``` LEFT { MATRIX {{ }#
{ }#
{ }}} MATRIX { { }& {1`````````````````` e= e^0 }& { }#
{ }& { }& { }#
{ }& {0``````````````````e != e^0 }& { } }
int E^0 (e) ``=``` LEFT { MATRIX {{ }#
{ }#
{ }}} MATRIX { { }& {1`````````````````` int e= int e^0 }& { }#
{ }& { }& { }#
{ }& {0`````````````````` int e != int e^0 }& { } }
(식7)
여기서, 식 (3.7)을 퍼지 싱글톤이라 한다. 식 (6)에 식 (7)을 대입하면 다음과 같다.
U^0 (u) = (e^0 , int e^0 , u)
(식8)
식 (식4)와 식 (식5)를 식 (식8)에 대입하면 다음과 같다.
R(e^0 , int e^0 , u)` = `R_1 (e^0 , int e^0 , u)`` BIGVEE ``R_2 (e^0 , int e^0 , u) ``BIGVEE ``CDOTS`` BIGVEE ``R_n (e^0 , int e^0 , u)
R_i (e^0 , int e^0 , u)` = `E_i (e^0 )`` BIGWEDGE `` int E_i ( int e^0 ) `` BIGWEDGE ``U_i (u)
(식9)
그러므로 적합도는 다음과 같다.
omega _i = E_i (e^0 ) BIGWEDGE int E_i ( int e^0 )
(식10)
여기서
omega _i
는 i번째 규칙의 전체 집합에 대한 적합도이다.
그러므로 식 (9)은 다음과 같다.
U^0 (u) = [ omega _1 BIGWEDGE U_1 (u)]`` BIGVEE`` [ omega _2 BIGWEDGE U_2 (u)]`` BIGVEE ``cdots``bigvee``[ omega _n BIGWEDGE U_n (u)]
= BIGVEE from { {i }=1} to n [ omega _i BIGWEDGE U_i (u)]
(식11)
식 (11)에서 i번째 항
omega _i ``BIGWEDGEB_i (u)
는 i번째의 규칙에 의한 추론 결과이다. 식(8)과 식(9)에 의해 다음과 같은 결과를 얻을 수 있다.
R_i (e^0 , int e^0 , u) = omega _i ``BIGWEDGE``U_i (u)
(식12)
7 비퍼지화
퍼지 규칙들로부터 추론된 최종적인 결론 값은 결정적인 값이 아니므로 프로세스의 입력으로 사용하기 위해서는 결정론적인 하나의 실수 값으로 만들어야 한다. 이러한 과정을 비퍼지화라 한다. 현재 일반적으로 사용하고 있는 방법에는 다음과 같은 것들이 있다.
첫쩨, 최대 평균법(mean of maxima) : 최대 맴버쉽을 갖는 원소의 ui의 평균을 취하는 방법이다.
u^0 = SUM from { { i}=0} to n u_i over i
(식13)
둘째, 최대 최소 평균법(average of maximum and minimum) : 최대 멤버쉽을 갖는 모든 원소의 uk 와 최소 멤버쉽 값을 갖는 원소의 ui 와의 사이에서 평균을 취하는 방법이다
u^0 = {u_i + u_k} over 2
(식14)
셋째, 무게 중심법(center of gravity) : 멤버쉽 함수의 값을 갖는 모든 요소들의 무게 중심을 취하는 방법이다. 일반적으로 가장 많이 사용되며 본 논문에서도 이 방법을 사용하고 있다. 이산화 집합의 경우는 다음과 같다.
u^0 = {SUM from { {i }=0} to n u_i ``` omega _i} over {SUM from { {i }=0} to n omega _i }
(식15)
그림 3.2는 추론 과정을 나타낸 것으로, 입력
e^0
와
int e^0
에 대하여 첫 번째 규칙에서는 오차와 오차 적분치의 멤버쉽 함수
E_1 ``와 ``int E_1
에서 적합도
omega _1
이 결정되며 제어 입력은
U_1
에서의 빗금친 부분이 된다. 두 번째 규칙에서도
E_1 ``와`` int E_2`` 에서`` omega _2
가 결정되며 제어 입력은
U_2
에서 의 빗금친 부분이 된다. 최종 제어입력
u^0
는 두 개의 제어입력의 무게중심으로 구해진다.
그림 2 추론 과정
예제) 6.16
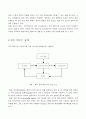
그림6.20 시뮬링크 블록다이어그램
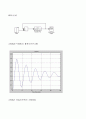
그림6.21 단일피드백의 스텝응답
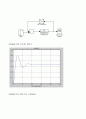
그림6.22 PID 피드백 제어기
그림6.23 PD 제어기의 스텝응답
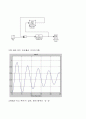
그림 6.25 퍼지 컨트롤러 다이어그램
그림6.27 FLC 제어기( 입력, 출력 범위는 -2∼2)
그림6.28 FLC 제어기( 입력 범위: 0∼0.7 , 출력 범위: -0∼2)
그림6.29 FLC 제어기( 입력: 0∼0.7 , 출력 범위는 0∼5.5)
◎룰 베이스
1. 입력이 low 이면, 출력이 low
2. 입력이 medium 이면, 출력이 medium
3. 입력이 high 이면, 출력이 high
◎입력과 출력의 MF
RN : IF eN is EN and
int`
eN is
int`
EN THEN uN is UN (식3)
식 (3)에서 E,
int`
E, U는 퍼지 변수이다. 그리고 제어 규칙의 전건부 e,
int`
e는 퍼지 제어기의 입력이며, 후건부의 u는 출력이다. 이때 i번째 제어규칙은 다음과 같다.
Ri = ( Ei
int`
Ei ) Ui (식4)
제어규칙들은 or 결합이기 때문에 n개의 제어규칙은 다음과 같다.
R = R1 R2 R3 ... RN =
BIGCUP from {{i}=1~} to n
Ri (식5)
입력을
E ^0 , INT E^0
라고 하면 출력
U^0
는 다음과 같다.
U^0 = R CIRC (E^0 TIMES INT E^0 )
##U^0 (u) = max[R(e, int e,u)`` BIGWEDGE `` E^0 (e) ``BIGWEDGE`` INT E^0 ( INT e)]
(식6)
여기서,
e^0 와 ~ TRIANGLE e^0
를 측정된 일반화된 수치라 하면 식 (6)에서
E^0
와
INT E^0
는 다음과 같다.
E^0 (e) ``=``` LEFT { MATRIX {{ }#
{ }#
{ }}} MATRIX { { }& {1`````````````````` e= e^0 }& { }#
{ }& { }& { }#
{ }& {0``````````````````e != e^0 }& { } }
int E^0 (e) ``=``` LEFT { MATRIX {{ }#
{ }#
{ }}} MATRIX { { }& {1`````````````````` int e= int e^0 }& { }#
{ }& { }& { }#
{ }& {0`````````````````` int e != int e^0 }& { } }
(식7)
여기서, 식 (3.7)을 퍼지 싱글톤이라 한다. 식 (6)에 식 (7)을 대입하면 다음과 같다.
U^0 (u) = (e^0 , int e^0 , u)
(식8)
식 (식4)와 식 (식5)를 식 (식8)에 대입하면 다음과 같다.
R(e^0 , int e^0 , u)` = `R_1 (e^0 , int e^0 , u)`` BIGVEE ``R_2 (e^0 , int e^0 , u) ``BIGVEE ``CDOTS`` BIGVEE ``R_n (e^0 , int e^0 , u)
R_i (e^0 , int e^0 , u)` = `E_i (e^0 )`` BIGWEDGE `` int E_i ( int e^0 ) `` BIGWEDGE ``U_i (u)
(식9)
그러므로 적합도는 다음과 같다.
omega _i = E_i (e^0 ) BIGWEDGE int E_i ( int e^0 )
(식10)
여기서
omega _i
는 i번째 규칙의 전체 집합에 대한 적합도이다.
그러므로 식 (9)은 다음과 같다.
U^0 (u) = [ omega _1 BIGWEDGE U_1 (u)]`` BIGVEE`` [ omega _2 BIGWEDGE U_2 (u)]`` BIGVEE ``cdots``bigvee``[ omega _n BIGWEDGE U_n (u)]
= BIGVEE from { {i }=1} to n [ omega _i BIGWEDGE U_i (u)]
(식11)
식 (11)에서 i번째 항
omega _i ``BIGWEDGEB_i (u)
는 i번째의 규칙에 의한 추론 결과이다. 식(8)과 식(9)에 의해 다음과 같은 결과를 얻을 수 있다.
R_i (e^0 , int e^0 , u) = omega _i ``BIGWEDGE``U_i (u)
(식12)
7 비퍼지화
퍼지 규칙들로부터 추론된 최종적인 결론 값은 결정적인 값이 아니므로 프로세스의 입력으로 사용하기 위해서는 결정론적인 하나의 실수 값으로 만들어야 한다. 이러한 과정을 비퍼지화라 한다. 현재 일반적으로 사용하고 있는 방법에는 다음과 같은 것들이 있다.
첫쩨, 최대 평균법(mean of maxima) : 최대 맴버쉽을 갖는 원소의 ui의 평균을 취하는 방법이다.
u^0 = SUM from { { i}=0} to n u_i over i
(식13)
둘째, 최대 최소 평균법(average of maximum and minimum) : 최대 멤버쉽을 갖는 모든 원소의 uk 와 최소 멤버쉽 값을 갖는 원소의 ui 와의 사이에서 평균을 취하는 방법이다
u^0 = {u_i + u_k} over 2
(식14)
셋째, 무게 중심법(center of gravity) : 멤버쉽 함수의 값을 갖는 모든 요소들의 무게 중심을 취하는 방법이다. 일반적으로 가장 많이 사용되며 본 논문에서도 이 방법을 사용하고 있다. 이산화 집합의 경우는 다음과 같다.
u^0 = {SUM from { {i }=0} to n u_i ``` omega _i} over {SUM from { {i }=0} to n omega _i }
(식15)
그림 3.2는 추론 과정을 나타낸 것으로, 입력
e^0
와
int e^0
에 대하여 첫 번째 규칙에서는 오차와 오차 적분치의 멤버쉽 함수
E_1 ``와 ``int E_1
에서 적합도
omega _1
이 결정되며 제어 입력은
U_1
에서의 빗금친 부분이 된다. 두 번째 규칙에서도
E_1 ``와`` int E_2`` 에서`` omega _2
가 결정되며 제어 입력은
U_2
에서 의 빗금친 부분이 된다. 최종 제어입력
u^0
는 두 개의 제어입력의 무게중심으로 구해진다.
그림 2 추론 과정
예제) 6.16
그림6.20 시뮬링크 블록다이어그램
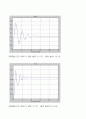
그림6.21 단일피드백의 스텝응답
그림6.22 PID 피드백 제어기
그림6.23 PD 제어기의 스텝응답
그림 6.25 퍼지 컨트롤러 다이어그램
그림6.27 FLC 제어기( 입력, 출력 범위는 -2∼2)
그림6.28 FLC 제어기( 입력 범위: 0∼0.7 , 출력 범위: -0∼2)
그림6.29 FLC 제어기( 입력: 0∼0.7 , 출력 범위는 0∼5.5)
◎룰 베이스
1. 입력이 low 이면, 출력이 low
2. 입력이 medium 이면, 출력이 medium
3. 입력이 high 이면, 출력이 high
◎입력과 출력의 MF
추천자료
 로켓(rocket)의 기본 이론
로켓(rocket)의 기본 이론 하이인리 도미노 연쇄 이론
하이인리 도미노 연쇄 이론 자기 센서의 원리 및 이론
자기 센서의 원리 및 이론 기계공작법(절삭이론) 학습지도안
기계공작법(절삭이론) 학습지도안 신체 운동에 대한 체육학 이론의 배경
신체 운동에 대한 체육학 이론의 배경 가족치료의 지적 기반이 되는 사이버네틱스 이론의 중요 개념들에 대해서 조사하고 사이버네...
가족치료의 지적 기반이 되는 사이버네틱스 이론의 중요 개념들에 대해서 조사하고 사이버네... 3. 피아제(piaget) 인지발달이론
3. 피아제(piaget) 인지발달이론 제7강 프로이드(Freud)의 정신분석이론 02.ppt
제7강 프로이드(Freud)의 정신분석이론 02.ppt 로보틱스 목적, 이론 방법
로보틱스 목적, 이론 방법 태브닌, 노턴의 정리와 최대전력전달 이론 전전설 결과 리포트
08
태브닌, 노턴의 정리와 최대전력전달 이론 전전설 결과 리포트
08 국제여론 - 형성 - 문제점 - 사례 마이클잭슨 - 사례 중동의 봄의 촉매제 튀니지 - 미디어의 ...
국제여론 - 형성 - 문제점 - 사례 마이클잭슨 - 사례 중동의 봄의 촉매제 튀니지 - 미디어의 ... 보육과정의 운영에 있어 행동주의 이론을 교육현장에 활용하는 것의 긍정적인 영향과 부정적...
보육과정의 운영에 있어 행동주의 이론을 교육현장에 활용하는 것의 긍정적인 영향과 부정적... 노화의 학설과 원인, 그리고 노화이론에 대해 기술하시오
노화의 학설과 원인, 그리고 노화이론에 대해 기술하시오





























소개글