이동평균법을 이용한 노이즈 제거

소개글

이동평균법을 이용한 노이즈 제거에 대한 보고서 자료입니다.

목차

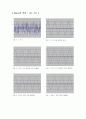
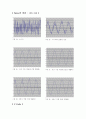
【 이동 평균법을 이용하여 신호의 노이즈 제거 】

본문내용

X*2-1)/10;
fx1=sin(2*pi*double(i)/50);
fx2[i]=noise+fx1;
fprintf(out1,"%10f\n",noise);
fprintf(out2,"%10f\n",fx1);
fprintf(out3,"%10f\n",fx2[i]);
}
for(i=3;i<197;i++) {
fx3=0;
for(j=-3;j<=3;j++)
fx3=fx3+fx2[i+j];
fx3=fx3/7;
fprintf(out4,"%10f\n",fx3);
}
for(i=10;i<190;i++) {
fx4=0;
for(j=-10;j<=10;j++)
fx4=fx4+fx2[i+j];
fx4=fx4/21;
fprintf(out5,"%10f\n",fx4);
}
w[0]=w[6]=-2;
w[1]=w[5]=3;
w[2]=w[4]=6;
w[3]=7;
for(i=3;i<197;i++) {
fx5=0;
for(j=-3;j<=3;j++)
fx5=fx5+fx2[i+j]*w[j+3];
fx5=fx5/21;
fprintf(out6,"%10f\n",fx5);
}
w[0]=w[20]=-171;
w[1]=w[19]=-76;
w[2]=w[18]=9;
w[3]=w[17]=84;
w[4]=w[16]=149;
w[5]=w[15]=204;
w[6]=w[14]=249;
w[7]=w[13]=284;
w[8]=w[12]=309;
w[9]=w[11]=324;
w[10]=329;
for(i=10;i<190;i++) {
fx6=0;
for(j=-10;j<=10;j++)
fx6=fx6+fx2[i+j]*w[j+10];
fx6=fx6/3059;
fprintf(out7,"%10f\n",fx6);
}
fclose(out1);
fclose(out2);
fclose(out3);
fclose(out4);
fclose(out5);
fclose(out6);
fclose(out7);
}
【 신호의 진폭 영역 해석 】
- Random한 신호에 대하여 평균, 분산, 중심 모멘트, 첨도, 외도 해석
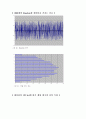
[ 1000개의 Random한 데이터를 가지는 신호 ]
그림 . Random 함수
그림 . 확률 밀도 함수
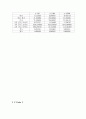
[ 데이터의 갯수(n)에 따른 랜덤 함수의 진폭 특성 ]
n=100
n=1000
n=10000
평균
-0.115024
0.048643
-0.022719
제곱 평균
21.450066
20.848654
22.453636
분산
21.436836
20.846287
22.453119
3차 중심 모멘트
9.723752
-0.118052
-1.356755
4차 중심 모멘트
1034.576050
934.520569
1043.099609
5차 중심 모멘트
988.186218
62.115200
-113.284592
첨도
3.834155
4.244663
3.802814.
왜도
-0.000001
0.000205
0.000009
[ C Code ]
#include
#include
#include
main()
{
FILE *out1,*out2;
float x,old_x,slope,p[20]={0},mean,moment[6],square,kurtosis,skewness;
int i,j,e1,e2;
out1=fopen("fx.dat","w");
out2=fopen("pdf.dat","w");
randomize();
old_x=(double)rand()/RAND_MAX*2-1;
fprintf(out1,"%f\n",old_x);
for(j=0;j<20;j++) {
if(((-1+0.1*(float)j)<=old_x)&((-1+0.1*(float)(j+1))>old_x))
e1=j;
}
for(i=0;i<10000;i++) {
x=(double)rand()/RAND_MAX*2-1;
fprintf(out1,"%f\n",x);
slope=x-old_x;
for(j=0;j<20;j++) {
if(((-1+0.1*(float)j)<=x)&((-1+0.1*(float)(j+1))>x))
e2=j;
}
if(e1==e2) p[e1]=p[e1]+1;
else {
if(slope>0) {
p[e1]=p[e1]+((-1+0.1*(float)(e1+1))-old_x)/slope;
p[e2]=p[e2]+(x-(-1+0.1*(float)e2))/slope;
for(j=(e1+1);j p[j]=p[j]+0.1/slope;
}
if(slope<0) {
p[e1]=p[e1]+((-1+0.1*(float)e1)-old_x)/slope;
p[e2]=p[e2]+(x-(-1+0.1*(float)(e2+1)))/slope;
for(j=(e2+1);j p[j]=p[j]-0.1/slope;
}
}
old_x=x; e1=e2;
}
for(i=19;i>=0;i--) {
p[i]=p[i]/10000/0.1;
fprintf(out2,"%f\n",p[i]);
}
fclose(out1);
fclose(out2);
mean=0;
for(i=0;i<20;i++)
mean=mean+(i-10+0.5)*p[i]*0.1;
printf("\n mean = %15f\n",mean);
for(j=2;j<6;j++) {
moment[j]=0;
for(i=0;i<20;i++) {
moment[j]=moment[j]+pow((i-10+0.5)-mean,j)*p[i]*0.1;
}
printf("%d central moment = %15f\n",j,moment[j]);
}
square=0;
for(i=0;i<20;i++)
square=square+(i-10+0.5)*(i-10+0.5)*p[i]*0.1;
printf(" mean square = %15f\n",square);
kurtosis=0; skewness=0;
for(i=0;i<20;i++) {
kurtosis=kurtosis+pow((i-10+0.5),4)*0.1/moment[4];
skewness=skewness+pow((i-10+0.5),3)*0.1/moment[3];
}
printf(" kurtosis = %15f\n",kurtosis);
printf(" skewness = %15f\n",skewness);
}

키워드

이동평균법,   노이즈,   필터링,   신호처리,   C 프로그램,   디지털