DFT DSP실험 사전보고서

목차

1. 실험 목적
2. 이 론
3. MATLAB을 이용한 신호분석

본문내용

의 이산값이라고 하면, 그 주파수 영역에의 변환결과
(복소수)도 [그림 4]에 나타낸 것과 같이 N개의 이산값이 되고, 그것을 X(0), X(1), X(2), ....., X(N-)
로 하면, 다음의 관계가 성립한다.
[식 G-5]
위의 수식이 DFT의 기본 수식이다. 적분기호가 제거되고, 덧셈의 식(sum)이 되었지만, 회전자 라고
하는 W는 처리하기 곤란한 항이다. 그래서, 이 W를 오일러 공식을 이용하여 다음과 같이 변환한다.
[식 G-6] 오일러 공식
FFT
위의 [식 G-6]을 [식 G-5]에 대입하면, 삼각함수와 곱셈의 덧셈연산이 되므로 컴퓨터를 이용한 연산이
가능하게 되었지만, 그 연산량은 상당히 방대하게 된다. 이 방대한 연산 시간문제를 해결하기 위하여,
고안된 변환이 고속 퓨리에 변환(FFT:Fast Fourier Transform)이다.
자료출처 : http://vision.inchon.ac.kr/binary_p13.html
3. MATLAB을 이용한 신호분석
7. 실험 2의 정현파를 Fourier Transform 한결과와 실험 5의 구형파를 Fourier Transform한 결과를
그래프로 나타내고 서로 다른 점을 분석하라.
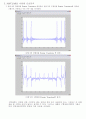
<실험 2의 정현파를 Fourier Transform 한 결과>
<실험 5의 구형파를 Fourier Transform한 결과>
구형파에는 정현파 성분 이외에도 많은 정현파 성분 등이 포함되어 있고, 그것들이 다 더해
졌을 때 구형파 신호가 된다고 생각할 수 있다. 그러므로 아래의 구형파를 FFT한 그림은
위의 정현파를 FFT한 결과와 다른 모습을 나타낸다.

키워드

DFT,   FFT,   MATLAB