본문내용
시간에 대한 변화를 결정하는 미분 방정식이다.
이 식의 초기 조건은 t = 0 , q = 0라는 조건이 성립한다.
이 식의 해는
이 식은 커패시터에서의 전하 q의 시간에 따른 변화를 나타내 주는 식이다.
이 식을 시간 d/dt로 미분을 하게되면 이 되어 전류의 시간적 변화를 나타내게 된다.
실험적으로 q(t)의 값은 커패시터 사이의 퍼텐셜 차를 측정하므로 측정할 수 있다.
마찬가지로 저항 사이의 퍼텐셜 차를 측정하면 i(t)를 측정 할 수 있다.
을 얻을 수 있다. 어떤 순간에도 의 합은 기전력ε 와 같음을 알 수 있다.
지수e에 나타나는 량은 차원이 없어야 하므로 RC는 시간의 차원을 갖는다. RC을 회로의 용량형 시간 상수라고 하며 τ라는 기호를 사용하여 나타낸다. 시간 상수는 커패시터가 완전히 충전되어 평형 상태에 도달했을 때의 전하량의 의 63%가 충전되는데 걸리는 시간이다.
충전 과정은 기기의 스위치를 닫으면 커패시터에는 아무 전하도 없음으로 판 사이에는 퍼텐셜 차가 생기지 않는다. 그러므로 회로의 법칙을 사용하면 저항 사이의 퍼텐셜 차는 기전력ε 와 같고 저항에 흐르는 전류는 ε/R이다.
이 결과는 전류가 흐르기 시작한 순간에만 맞는다. 왜냐하면 그 이후에는 커패시터 판 사이에 전하가 쌓여서 그 사이에 q/C의 퍼텐셜 차가 생기기 때문이다. 회로의 법칙을 사용하면 이렇게 전하가 쌓이는 과정에서 저항과 커패시터의 퍼텐셜 합은 전지의 기전력과 같아야 하므로 저항의 퍼텐셜 차는 감소하므로 전류도 줄어든다.
저항에서의 전류의 변화는 커패시터가 완전히 충전될 때까지 계속된다. 완전히 충전되었다는 것은 커패시터의 퍼텐셜 차가가 전지의 기전력과 같다는 것을 말한다.
그렇다면 방전이 될 때는 전류가 시간에 대해서 어떻게 변할 것인다.
ε = 0이라고 놓으면
이 방정식의 해는이고 는 처음에 커패시터가 완전히 충전되었을 때의 전하이다.
전기 용량 시간 상수 RC는 충전할 때뿐만 아니라 방전할 때도 중요한 역할을 한다. t = RC 일 때 커패시터의 전하는 약 37%인 로 줄어든다.
방전 과정에서의 전류는 을 얻는다. 여기서 는 t=0에 해당하는 처음 전류이다.
고정된 전원 전압 하에서 저항을 통하여 커패시터가 충전되는 경우에 시간에 따른 전류는 키르히호프의 법칙으로 결정될 수 있다.
----------------------- ⑴
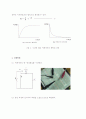
그림 2. 시간에 따른 커패시터의 충방전 과정
4. 실험방법
(1) 커패시터의 충ㆍ방전회로를 구성한다.
(2) 충전 과정에 있어서의 파형을 오실로스코프로 확인한다.
5. 실험결과
(1) 오실로스코프에 잠깐 파형이 나타났으나 너무 짧은 순간만 유지 되었다.
6. 고찰
이번 실험은 저항과 커패시터로 이루어진 RC회로의 충,방전시 파형을 알아보기 위한 실험이었다.
잠깐이지만 결과는 이론에서 보았던 그래프와 거의 같은 모습을 보였다. 중간에서 매끄럽지 못하고 약간 곡선이 흔들렸는데 이는 회로의 접속이 약간 좋지 않았거나 회로의 다른 구성품들 내부에 문제가 조금 있었던 것 같다. 그렇게 심하진 않아서 만족할 만하다.
이 식의 초기 조건은 t = 0 , q = 0라는 조건이 성립한다.
이 식의 해는
이 식은 커패시터에서의 전하 q의 시간에 따른 변화를 나타내 주는 식이다.
이 식을 시간 d/dt로 미분을 하게되면 이 되어 전류의 시간적 변화를 나타내게 된다.
실험적으로 q(t)의 값은 커패시터 사이의 퍼텐셜 차를 측정하므로 측정할 수 있다.
마찬가지로 저항 사이의 퍼텐셜 차를 측정하면 i(t)를 측정 할 수 있다.
을 얻을 수 있다. 어떤 순간에도 의 합은 기전력ε 와 같음을 알 수 있다.
지수e에 나타나는 량은 차원이 없어야 하므로 RC는 시간의 차원을 갖는다. RC을 회로의 용량형 시간 상수라고 하며 τ라는 기호를 사용하여 나타낸다. 시간 상수는 커패시터가 완전히 충전되어 평형 상태에 도달했을 때의 전하량의 의 63%가 충전되는데 걸리는 시간이다.
충전 과정은 기기의 스위치를 닫으면 커패시터에는 아무 전하도 없음으로 판 사이에는 퍼텐셜 차가 생기지 않는다. 그러므로 회로의 법칙을 사용하면 저항 사이의 퍼텐셜 차는 기전력ε 와 같고 저항에 흐르는 전류는 ε/R이다.
이 결과는 전류가 흐르기 시작한 순간에만 맞는다. 왜냐하면 그 이후에는 커패시터 판 사이에 전하가 쌓여서 그 사이에 q/C의 퍼텐셜 차가 생기기 때문이다. 회로의 법칙을 사용하면 이렇게 전하가 쌓이는 과정에서 저항과 커패시터의 퍼텐셜 합은 전지의 기전력과 같아야 하므로 저항의 퍼텐셜 차는 감소하므로 전류도 줄어든다.
저항에서의 전류의 변화는 커패시터가 완전히 충전될 때까지 계속된다. 완전히 충전되었다는 것은 커패시터의 퍼텐셜 차가가 전지의 기전력과 같다는 것을 말한다.
그렇다면 방전이 될 때는 전류가 시간에 대해서 어떻게 변할 것인다.
ε = 0이라고 놓으면
이 방정식의 해는이고 는 처음에 커패시터가 완전히 충전되었을 때의 전하이다.
전기 용량 시간 상수 RC는 충전할 때뿐만 아니라 방전할 때도 중요한 역할을 한다. t = RC 일 때 커패시터의 전하는 약 37%인 로 줄어든다.
방전 과정에서의 전류는 을 얻는다. 여기서 는 t=0에 해당하는 처음 전류이다.
고정된 전원 전압 하에서 저항을 통하여 커패시터가 충전되는 경우에 시간에 따른 전류는 키르히호프의 법칙으로 결정될 수 있다.
----------------------- ⑴
그림 2. 시간에 따른 커패시터의 충방전 과정
4. 실험방법
(1) 커패시터의 충ㆍ방전회로를 구성한다.
(2) 충전 과정에 있어서의 파형을 오실로스코프로 확인한다.
5. 실험결과
(1) 오실로스코프에 잠깐 파형이 나타났으나 너무 짧은 순간만 유지 되었다.
6. 고찰
이번 실험은 저항과 커패시터로 이루어진 RC회로의 충,방전시 파형을 알아보기 위한 실험이었다.
잠깐이지만 결과는 이론에서 보았던 그래프와 거의 같은 모습을 보였다. 중간에서 매끄럽지 못하고 약간 곡선이 흔들렸는데 이는 회로의 접속이 약간 좋지 않았거나 회로의 다른 구성품들 내부에 문제가 조금 있었던 것 같다. 그렇게 심하진 않아서 만족할 만하다.
키워드
추천자료
 기계공학실험 휘스톤브리지
기계공학실험 휘스톤브리지 평형브리지회로
평형브리지회로 실험20. 전기저항측정 - 휘스톤브리지 Wheatstone Bridge
실험20. 전기저항측정 - 휘스톤브리지 Wheatstone Bridge MMORPG의 평균체류시간 요인분석_석사논문
MMORPG의 평균체류시간 요인분석_석사논문 2.4 휘스톤브리지를 이용한 전기저항 측정 -예비
2.4 휘스톤브리지를 이용한 전기저항 측정 -예비 MLB모자 마케팅 전략 - F&F 마케팅전략 분석 보고서
MLB모자 마케팅 전략 - F&F 마케팅전략 분석 보고서 제주도 리조트 발전역사 및 분포 특성
제주도 리조트 발전역사 및 분포 특성 예비6휘스톤 브리지 예비레포트
예비6휘스톤 브리지 예비레포트 실험보고서 - 휘스톤 브리지와 스트레인 게이지 회로 실험
실험보고서 - 휘스톤 브리지와 스트레인 게이지 회로 실험 물리실험보고서 - 휘스톤 브리지를 이용한 전기저항 측정
물리실험보고서 - 휘스톤 브리지를 이용한 전기저항 측정 휘트스톤 브리지 (Wheatstone bridge) - 물질의 전기적 특성의 하나인 전기저항이 실제로 어...
휘트스톤 브리지 (Wheatstone bridge) - 물질의 전기적 특성의 하나인 전기저항이 실제로 어... 일반물리학 실험 - 휘스톤 브리지를 이용한 전기저항 측정
일반물리학 실험 - 휘스톤 브리지를 이용한 전기저항 측정 [일반물리학 실험] 휘스톤브리지(휘트스톤브리지/Wheatstone Bridge)를 이용한 전기저항 측정...
[일반물리학 실험] 휘스톤브리지(휘트스톤브리지/Wheatstone Bridge)를 이용한 전기저항 측정... 물리학 실험 보고서 휘스턴 브리지를 이용한 전기저항 측정 실험
물리학 실험 보고서 휘스턴 브리지를 이용한 전기저항 측정 실험




























소개글