흙의 압밀 시험( 결과 고찰 포함)

목차

1. 서 론
2. 본 론
3. 결 언

본문내용

하고 흙 입자만의 가상높이 2Hs라고 하면 그때의 간극비 ef는 다음과 같다.
여기에서, Ws : 흙의 건조무게 [gf/cm3]
윗 식을 이용하면 간극비 e와 압밀압력 p와의 관계곡선 (p-e)을 얻을 수 있다.
②함수비 w의 계산
압밀이 완료되었을 때의 함수비 wf는 공시체를 노건조하여 측정할 수 있다.
여기서, W2 : 입밀이 완료된 후의 공시체무게 [gf]
W3 : 압밀이 완료된 공시체 W2를 건조시킨 후의 무게 [gf]
③포화도 S의 계산
포화도 S는 압밀이 시작되기 전의 포화도 Sr0와 끝난 후의 포화도 Srf로 구분하여 압밀 시작 전의 함수비 w0와 압밀 끝난 후의 함수비 wf로부터 계산한다.
여기서 Sr0 : 압밀 시작 전의 초기 포화도
Srf : 압밀이 끝난 후의 포화도
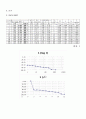
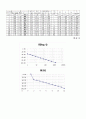
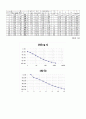
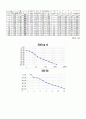
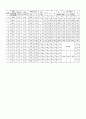
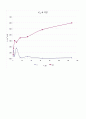
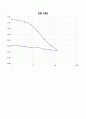
3.2.5 압밀하중 p와 간극비 e의 관계
압밀하중 p와 간극비 e의 관계를 나타내기 위하여 세로축에 간극비 e, 가로축에 압밀하중 p를 반대수로 그리면 logp-e곡선이 되고 이 곡선의 처음부분은 기울기가 완만하게 나타나지만, 어느 압력 이상이 되면 갑자기 급해져서 거의 직선상을 보이는데 그 경계가 되는 압력을 선행압밀압력(preconsolidation pressure)p0이라고 한다. 선행압밀압력은 지반이 과거에 받았던 하중을 나타내며, 그 크기는 그 흙의 응력경로에 의존한다.
① 선행압밀하중((preconsolidation pressure, p0)
Casagrande(1936)는 선행압밀하중 p0을 결정하는 방법을 다음과 같이 제시하고 있다.
가. 압력-간극비 곡선(logp-e)에서 곡률이 가장 큰 점 P를 선택하여 그 점을 통과하는 수평선과 접선을 긋는다.
나. 이 두 선분으로 이루어지는 각도를 2등분한 선이 이 곡선의 직선 부분의 연장선과 만나는 점 T에 대응하는 압력이 선행압밀압력 p0가 된다.
선행압밀하중 P0은 점토의 특성을 아는데 있어서 대단히 중요하다. 만일 압밀시험일 실시한 흙시료가 과거 어떤 시기에 현재보다 더 큰 압력을 받은 적이 있었 다면, 압밀곡선으로부터 구한 선행압밀하중의 값은 그 시료가 현제 받고 있는 연직압력보다 더 큰 값을 보인다. 이런 경우 그 시료는 과압밀 (over consolidat
ed)되었다고 하며, 선행압밀압력의 현재 받고 있는 연직압력에 대한 비를 과압밀비(Over- Consolidation Ratio, OCR)라고 한다. 전자와 후자가 동일하다면 그 흙은 정규 압밀상태(normal consolidation state)에 있다고 말한다.
② 압축계수 (av : coefficient of compressibilify), 압축지수(compression index, Cc)
압축계수 av는 압밀압력-간극비(p-e)곡선의 기울기를 나타내며 다음의 식으로 표현된다.
e-logp곡선에서 직선 부분의 기울기를 압축지수(compression index, Cc)라 하며, 다음의 식으로 표현된다.
압축계수 av와 압축지수 Cc는 연약할수록 크고 견고할수록 작으며, 압밀침하량을 계산하는데 쓰이는 중요한 값이다. 압력이 증가하면 부피가 감소하므로 부(負)의 기호를 붙이면 압축계수 av와 압축지수 Cc는 결국 정의 값을 가진다.
③ 체적변화계수(Coefficient of volume change, mv)
체적변화계수 mv는 유효 응력의 증가에 대한 부피변화율로 정의되며, 그 단위는 압력의 역수이다. 이것을 식으로 표현하면,
어떤 흙에 대한 mv의 값은 일정한 값이 아니며, 그 값은 계산하고자 하는 압력의 범위에 따라 달라진다.
④ 투수계수 k
투수계수 k도 각 하중단계의 압밀계수 Cv와 압축계수 av 및 체적변화계수 mv를 이용하여 계산할 수 있다.
4. 고 찰
1. 목 적
일반적으로 모든 흙은 압축성을 지니고 있지만, 점토와 같이 투수계수가 아주 작은 하중이 가해지면 과잉간극수압이 발생하게 되며, 이러한 영향으로 오랜시간에 걸쳐 흙 속에 있는 물이 빠져나가면서 지반이 압축되는 현상을 압밀이라고 한다.
이러한 점성토층의 침하속도 및 침하량의 계산이 필요한 자료를 얻고 점성토의 탄성범위와 소성범위의 한계응력을 표시하는 압밀항복응력을 구할 수 있으며 압밀상태, 투수계수 등도 간접적으로 구할 수 있다.
2. 시험의 오차
첫째로 압밀시험은 다른 시험과 달리 매우 장시간이 소요되고 정교함을 요하는 시험인데 시험을 하는데 있어서 추를 추가로 재하하여 줄 때 좀 더 조심스럽게 올리지 못해 올리는 과정에 있어서 오차가 발생하였을 것 같다. 두번째로 시험 기간이 길다 보니 측정을 하는데 있어 조원 네명이 번갈아 가면서 측정하여 그런지 정교함을 요하는 다이얼게이지 측정에 있어서 조원 개개인의 주관적인 판단으로 인한 오차가 발생할 수 있었을 것이다. 세번째로 시험 중간에 추가 모자라는 경우가 있어 여러추들을 조합하여 무게를 맞추어 재하한 경우도 있는데 이 때도 다른 조에 비해 오차가 발생 되었을 수 있을 것이다. 네번재로 24시간을 측정하고 추를 추가 재하하고 바로 1분에 측정하는 경우가 있는데 이 때는 무게를 더 추가하여 주기 때문에 침하량이 좀 큰 것이 사실이다. 이에 다이얼 게이지를 측정하는데 있어서 계속 눈금이 변하기 때문에 바로 측정값을 읽어내기가 어려워서 오차가 발생하였을 것 같다. 마지막으로 압밀 통에 물을 수시로 점검하여야 했는데 중간에 추석 연휴가 끼어 연휴를 마치고 실험을 하려할 때 물이 많이 증발한 상태였다. 여기서도 오차를 발생시킬 수 있었을 것이다.
3. 느 낀 점
실험을 하는데 있어서 우리 조가 다른 조에 비해 실험을 늦게 시작하였다. 그래서 실험 측정값을 읽는 시간이 늦으면 저녁 7시 넘어서도 실험실에 찾아와야 했고 실험자체가 계속 이어서 하는 것이라 주말에도 역시 실험실을 방문하여 해서 그런지 전체적인 실험은 별 어려운 점이 없었지만 너무 많은 시간을 요하는 실험이라 너무 힘들었던 것 같다. 이번 실험은 정교함이 무척이나 필요한 실험이었던 같다. 하지만 우리는 처음 하는 실험이라 조심스럽게 재하를 하고 다이얼게이지를 읽는데 있어서 좀 더 정확하게 읽으려 했는데 막상 그렇게 되지 않은 것 같다. 많은 시간을 투자한만큼 아쉬움이 많이 남는 실험이었다.

키워드

압밀,   흙,   압밀시험