물질 전달(Mass Transfer)

소개글

물질 전달(Mass Transfer)에 대한 보고서 자료입니다.

목차

1. 물질전달의 기본 원리

2. 물질전달과 확산

3. 기체의 분자 확산

4. 액체의 분자 확산

5. 고체의 분자 확산

6. 생물용매의 분자 확산

7. 확산계수

8. 대류 물질전달

9. 세공이 작은 구조에서의 기체 확산

본문내용

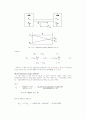
식이 있다. 그림 (1-9(a))와 같은 계단식 접촉조작에서는 두 상이 접촉하여 물질전달이 일어나는 장소를 단(stage)이라 하며, 두 상은 각 단에서 그 조성이 평형상태에 도달한 후에 각각 다음의 상하 단으로 이동한다. 각 단은 정체량에 대해 출입하는 양이 대단히 적어서 평형에 도달하는 조건과 시간이 문제되지 않고 발열 또는 흡열에 의한 열량의 증감이 없는 이상단(ideal stage)으로 생각한다. 그러나 실제로는 정체량에 대한 출입량이 적지 않으며 두 상 사이의 접촉도 충분하지 못하므로 평형상태에 도달하기 전에 다음 단으로 이동하게 된다. 따라서 물질전달에 필요한 실제단수는 이상단의 수, 즉 이론단수(number of theoritical srage)보다 많아진다. 실제단수에 대한 이론단수의 비를 단효율(stage efficience)이라 한다.
연속식 접촉조작에서는 그림 (1-9(b))에서는 두 상의 평형관계가 성립될 높이의 간격 AB를 가상해서 하나의 이론단에 상당하는 것으로 계산하며 이 높이가 낮을수록 효율이 좋다.
(a) (b)
그림. (1-9) 접촉조작 방식
그림 (1-10)은 다단 향류 접촉공정에 대한 이상단수를 구하는 방법이다.
그림. (1-10) 다단 향류 접촉 공정
전체 공정에 대한 총괄 물질수지 및 성분수지는 다음과 같다.
Lo + VN+1 = LN + V1 (1-75)
Loxo + VN+1yN+1 = LNxN + V1y1 (1-76)
여기서 L, V는 각각 액상 및 기상의 전달속도이며 x, y는 각각 액상의 몰분율과 기상의 몰분율을 나타낸다. 한편, 임의의 단 n까지에 대한 물질수지는
Lo + Vn+1 = Ln + V1 (1-77)
Loxo + Vn+1yn+1 = Lnxn + V1y1 (1-78)
조작선의 방정식은
(1-79)
따라서 각 단에 대한 x-y 관계화 조작선의 방정식을 가지고 작도하면 이상단수를 구할 수 있다. 그림 (1-11)은 4단 접촉공정에서의 단수작도 방법을 나타낸 것으로 삼각형의 수가 이론단수가 된다.
그림. (1-11) 다단 향류 접촉에서의 이론단수 계산 방법
[예제 16] 이론단수
향류 접촉탑에서 공기 중에 1.0[m%]의 아세톤이 포함된 기체로부터 아세톤의 90[%]를 물에 흡수한다. 출구에서의 기체 유속은 30[kg-mol/h], 물의 유속은 90[kg-mol/h]이다. 이 조작은 1[atm], 300[K]에서 이루어지며 기-액에서의 아세톤(A)에 대한 평형관계는 yA=2.53xA이다. 접촉탑의 이론단수를 구하라.
풀이) y1 = 0, yAN+1 = 0.01, xAo = 0, VN+1 = 30[kg-mol/h], Lo = 90[kg-mol/h]
들어가는 아세톤의 양 = VN+1yAN+1 = (30)(0.01) = 0.3[kg-mol/h]
들어가는 공기의 양 = VN+1(1-yAN+1) = (30)(0.09) = 29.7[kg-mol/h]
V1에 포함되어 나가는 아세톤 = (0.3)(0.1) = 0.03[kg-mol/h]
LN에 포함되어 나가는 아세톤 = (0.3)(0.9) = 0.27[kg-mol/h]
∴ V1 = 29.7 + 0.03 = 29.73[kg-mol/h]
yA1 = 0.03/29.73 = 0.001
LN = 90 + 0.27 = 90.27[kg-mol/h]
xAN = 0.27/90.27 = 0.003
따라서 Lo = 90[kg-mol/h]의 액체가 들어가서 LN = 90.27[kg-mol/h]의 액체가 출구로 나가며, 기체는 30[kg-mol/h]이 들어가서 29.73[kg-mol/h]이 나온다. 이상의 결과로부터 이론단수를 작도하면 다음 그림과 같으며 이론단수는 약 5.2단이다.
9. 세공이 작은 구조에서의 기체 확산
다공질 고체에서 기체나 액체가 확산되는 경우 세공이 크면 Fick 형태의 확산이 되고 세공이 작으면 다른 형태의 확산이 된다.
기체가 세공이 작은 구조에서 확산하는 예로는 가스가 작은 세공을 확산하여 촉매의 표면에서 반응하는 불균일 촉매 반응이나 고기를 냉동 건조할 때는 H2O가 다공 구조를 확산에 의해 빠져 나오는 것 들이 있다. 세공이 작은 구조에서의 확산은 세공 직경에 영향을 받는다.
기체 분자가 다른 기체 분자에 충돌하지 않고 다닐 수 있는 평균 거리인 평균 자유 행로 λ를 정의하면
(1-80)
λ : mean free path [m]
μ : 점도
P : 압력 [N/m2]
T : 온도 [K]
M : 분자량 [kg/kgmol]
R : 기체상수 8.3143*103 [Nm/kgmol K]]
낮은 압력에서 λ값은 크다. 그리고 액체의 경우 λ값이 작기 때문에 Fick의 법칙을 따른다.
기체의 크누센 확산
다음 그림은 전 압력 P가 일정할 때 입구에서 분압이 pA1인 기체 분자가 직경 dm의 모세관으로 확산하는 그림으론소 λ는 직경 d에 비해서 크다. 그러므로 분자는 벽에 부딪히며 분자와 벽간의 충돌이 물질전달에 중요한 역할을 하게 되는데 이런 경우를 크누센 확산이라 한다.
그림. (1-12) 가는 모세관에서 기체확산의 형태
크누센 확산 계수는 압력 P에 무관하고, 다음과 같이 계산한다.
(1-81)
DKA : 크누센 확산계수 [m2/s]
는 : 세공의 평균 반지름 [m]
: A성분의 평균 분자 속도 [m/s]
의 이론 속도식을 이용하면
(1-82)
MA는 A의 분자량으로 [kg/kgmol]이고, T는 온도 [K]이다.
세공내에서 크누센 확산의 플럭스 식은
(1-83)
z1 = 0, pA = pA1, z2 = L, pA = pA2로 적분하면,
(1-84)
물질 A의 크누센 확산은 물질 B와 충돌하는 것이 아니고 세공벽에 충돌하는 것이기 때문에 B와 전혀 관계가 없다.
크누센 수 NKn을 정의하면
(1-85)
여기서 NKn≥10이면 크누센 확산이라고 볼 수 있다.
[예제 17] 크누센 확산
H2(A)-C2H6(B)의 가스 혼합물이 니켈 촉매의 세공에서 수소 첨가 반응을 하고 있다. 압력 P는 1.0135*105Pa이고 온도 T는 373K이다. 세공의 반지름이 60Å일 때, 수소의 크누센 확산 계수 DKA를 구하라.
풀이) = 6.0×10-9m, MA = 2.016, T = 373K

키워드

Fick의 법칙,   일방확산,   등몰 상대확산,   분자 확산,   대류 물질전달,   고체의 분자 확산,   확산계수,   크누센 확산