목차
1.테일러다항식
2.이분법
3.선형보간법
4.소스코드
2.이분법
3.선형보간법
4.소스코드
본문내용
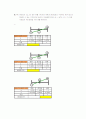
55
0.0672
0.4792
부호
-
+
+
버려질구간
하한
중간값
상한
x
1.3125
1.3593
1.4062
y
-0.3155
-0.1278
0.0672
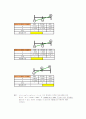
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3593
1.3828
1.4062
y
-0.1278
-0.0309
0.0672
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3828
1.3945
1.4062
y
-0.0309
0.0179
0.0672
부호
-
+
+
버려질구간
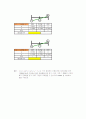
결론 . 식의 현재까지 이분법 계산과정을 보면
계산이 로 1.3828<<1.4062 구간에서 해가 존재함을 유추 할 수 있다. 계산이 오래걸릴 것 같으므로 Matlab 을 이용하여 해를 구해보자.
소스코드
실행결과 및 답
에서 오차범위 내의 해가 도출되었다.
#2-3
Do it. 임의의 비선형 함수 f(x)를 설정하고, 이를 선형보간법을 이용하여 푸시오.
접근 1. 설정된 임의의 함수 f(x)
--
접근 2. 설정된 함수 와 직선보간함수를 설정한다.
직선보간함수는 원함수의 설정된 구간의 하한과 상한의 값을 구하고 기울기를 구하여 설정한다.
--
원함수 :
직선보간함수 :
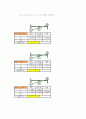
접근 3. 의 초기설정구간 에서의 해 존재유무를 판단해보자.
※ 해의 특성에 따라 이어야 해가 존재하는 구간이다.
--
하한
상한
x
0
3
y
-3
16.0680
부호
-
+
접근 4. 해의 특성에 따라 이어야 해가 존재한다.
선형보간함수 의 해는 0.4719이다. 이고 원함수에 이 값을 넣으면 -2.5096 이 나오므로 가되고 해는 0.4719 근처에 있다는 것을 유추할 수 있다. 구간으로 원함수인 의 해를 구하여보자
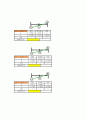
--
하한
중간값
상한
x
0.4179
0.8697
3
y
-2.5096
-1.7515
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
0.8697
1.1088
3
y
-1.7515
-1.0532
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.1088
1.2492
3
y
-1.0532
-0.5585
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.2492
1.3181
3
y
-0.5585
-0.2934
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3181
1.3517
3
y
-0.2934
-0.1587
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3517
1.3690
3
y
-0.1587
-0.0880
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3690
1.3783
3
y
-0.0880
-0.0496
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3783
1.3834
3
y
-0.0496
-0.0284
16.0680
부호
-
-
+
버려질구간
결론 . 식의 현재까지 선형보간법 계산과정을 보면
1.3834<<3 구간에서 해가 존재함을 유추 할 수 있다. 또한, 1.3834의 근처에 해가 존재함을 알 수 있다. 계산이 오래걸릴 것 같으므로 Matlab 을 이용하여 해를 구해보자.
소스코드
실행결과 및 답
에서 오차범위 내의 해가 도출되었다.
최종 결과
위의 결과에서 볼 수 있듯이 선형보간법을 사용하면 이분법 보다 빠르게 해를 찾을 수 있다. 그 이유는 직선보간함수를 이용한 해 의 의 값과 이전에 설정한 구간 a또는 b의 곱에 따라 버리는 구간이 생기고 그 이후로부터는 값과 구하려는 해는 근처에 위치해 있기 때문에 구간을 줄이는데 시간이 적게 든다. 즉, 이 성립하지 않는다면 해의 특성에 따라 해가 될 수 없다. 따라서 이야기 하고 싶은 점은 그 구간은 버려지게 되고 나머지 구간에서 아래의 그림처럼 직선보간함수와 원함수의 해가 가까이 있으므로 그다음 구간설정에 용이하다는 점이다.
- 그림 1.1 설정한 임의의 함수에 대한 그래프 -
% # 2 - 2 아래 # 2 - 3 있음
%설정한 함수 f(x)를 이용하여 f(x) = 0 를 만족하는 해를 이분법 및 Matlab을
%사용하여 구하시오. 답에는 소스 코드와 실행 결과 및 답을 명시하시오.
clear all
clc
f=\'((sin(x)).^3)+((cos(x)).^2)+exp(x)-5\'
n=0; a=0; b=3; c=(a+b)/2; err=0.0000001;
fprintf(\' L 하한X(l) 상한X(u) 해 오차 \\n\')
while b-c>=err
n=n+1;
x=b;
fb=eval(f);
x=c;
fc=eval(f);
if fb*fc<=0
a=c;
c=(a+b)/2;
else
b=c;
c=(a+b)/2;
end
fprintf(\'%5.0f %15.8f %15.8f %15.8f %20.8e \\n\',n, a, b, c, b-c)
end
fprintf(\'\\n 총 %2.0f 번 시행하여 나온결과 근사치는 %2.8f 이며, 오차는 %2.8e 입니다. \\n\',n, c, b-c);
% # 2 - 3
%위에서 설정한 함수 f(x)를 이용하여 f(x) = 0 를 만족하는 해를 선형보간법 및
%Matlab을 사용하여 구하시오. 답에는 소스 코드와 실행 결과 및 답을 명시하시오.
clear all
clc
f=\'((sin(x)).^3)+((cos(x)).^2)+exp(x)-5\'
n=0; a=0; b=3; err=0.0001;
x=a; fa=eval(f);
x=b; fb=eval(f);
c=b-fb*(a-b)/(fa-fb);
x=c; fc=eval(f);
fprintf(\' L 하한X(l) 상한X(u) 해 오차 \\n\')
while abs(fc)>=err
n=n+1;
x=a; fa=eval(f);
x=b; fb=eval(f);
c=b-fb*(a-b)/(fa-fb);
x=c; fc=eval(f);
if fa*fc<=0
b=c; c=b-fb*(b-a)/(fb-fa);
else
a=c; c=b-fb*(b-a)/(fb-fa);
end
fprintf(\'%5.0f %15.8f %15.8f %15.8f %20.8e \\n\',n, a, b, c, fc)
end
fprintf(\'\\n 총 %2.0f 번 시행하여 나온결과 근사치는 %2.8f 이며, 오차는 %2.8e 입니다. \\n\',n, c, b-c)
0.0672
0.4792
부호
-
+
+
버려질구간
하한
중간값
상한
x
1.3125
1.3593
1.4062
y
-0.3155
-0.1278
0.0672
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3593
1.3828
1.4062
y
-0.1278
-0.0309
0.0672
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3828
1.3945
1.4062
y
-0.0309
0.0179
0.0672
부호
-
+
+
버려질구간
결론 . 식의 현재까지 이분법 계산과정을 보면
계산이 로 1.3828<<1.4062 구간에서 해가 존재함을 유추 할 수 있다. 계산이 오래걸릴 것 같으므로 Matlab 을 이용하여 해를 구해보자.
소스코드
실행결과 및 답
에서 오차범위 내의 해가 도출되었다.
#2-3
Do it. 임의의 비선형 함수 f(x)를 설정하고, 이를 선형보간법을 이용하여 푸시오.
접근 1. 설정된 임의의 함수 f(x)
--
접근 2. 설정된 함수 와 직선보간함수를 설정한다.
직선보간함수는 원함수의 설정된 구간의 하한과 상한의 값을 구하고 기울기를 구하여 설정한다.
--
원함수 :
직선보간함수 :
접근 3. 의 초기설정구간 에서의 해 존재유무를 판단해보자.
※ 해의 특성에 따라 이어야 해가 존재하는 구간이다.
--
하한
상한
x
0
3
y
-3
16.0680
부호
-
+
접근 4. 해의 특성에 따라 이어야 해가 존재한다.
선형보간함수 의 해는 0.4719이다. 이고 원함수에 이 값을 넣으면 -2.5096 이 나오므로 가되고 해는 0.4719 근처에 있다는 것을 유추할 수 있다. 구간으로 원함수인 의 해를 구하여보자
--
하한
중간값
상한
x
0.4179
0.8697
3
y
-2.5096
-1.7515
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
0.8697
1.1088
3
y
-1.7515
-1.0532
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.1088
1.2492
3
y
-1.0532
-0.5585
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.2492
1.3181
3
y
-0.5585
-0.2934
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3181
1.3517
3
y
-0.2934
-0.1587
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3517
1.3690
3
y
-0.1587
-0.0880
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3690
1.3783
3
y
-0.0880
-0.0496
16.0680
부호
-
-
+
버려질구간
하한
중간값
상한
x
1.3783
1.3834
3
y
-0.0496
-0.0284
16.0680
부호
-
-
+
버려질구간
결론 . 식의 현재까지 선형보간법 계산과정을 보면
1.3834<<3 구간에서 해가 존재함을 유추 할 수 있다. 또한, 1.3834의 근처에 해가 존재함을 알 수 있다. 계산이 오래걸릴 것 같으므로 Matlab 을 이용하여 해를 구해보자.
소스코드
실행결과 및 답
에서 오차범위 내의 해가 도출되었다.
최종 결과
위의 결과에서 볼 수 있듯이 선형보간법을 사용하면 이분법 보다 빠르게 해를 찾을 수 있다. 그 이유는 직선보간함수를 이용한 해 의 의 값과 이전에 설정한 구간 a또는 b의 곱에 따라 버리는 구간이 생기고 그 이후로부터는 값과 구하려는 해는 근처에 위치해 있기 때문에 구간을 줄이는데 시간이 적게 든다. 즉, 이 성립하지 않는다면 해의 특성에 따라 해가 될 수 없다. 따라서 이야기 하고 싶은 점은 그 구간은 버려지게 되고 나머지 구간에서 아래의 그림처럼 직선보간함수와 원함수의 해가 가까이 있으므로 그다음 구간설정에 용이하다는 점이다.
- 그림 1.1 설정한 임의의 함수에 대한 그래프 -
% # 2 - 2 아래 # 2 - 3 있음
%설정한 함수 f(x)를 이용하여 f(x) = 0 를 만족하는 해를 이분법 및 Matlab을
%사용하여 구하시오. 답에는 소스 코드와 실행 결과 및 답을 명시하시오.
clear all
clc
f=\'((sin(x)).^3)+((cos(x)).^2)+exp(x)-5\'
n=0; a=0; b=3; c=(a+b)/2; err=0.0000001;
fprintf(\' L 하한X(l) 상한X(u) 해 오차 \\n\')
while b-c>=err
n=n+1;
x=b;
fb=eval(f);
x=c;
fc=eval(f);
if fb*fc<=0
a=c;
c=(a+b)/2;
else
b=c;
c=(a+b)/2;
end
fprintf(\'%5.0f %15.8f %15.8f %15.8f %20.8e \\n\',n, a, b, c, b-c)
end
fprintf(\'\\n 총 %2.0f 번 시행하여 나온결과 근사치는 %2.8f 이며, 오차는 %2.8e 입니다. \\n\',n, c, b-c);
% # 2 - 3
%위에서 설정한 함수 f(x)를 이용하여 f(x) = 0 를 만족하는 해를 선형보간법 및
%Matlab을 사용하여 구하시오. 답에는 소스 코드와 실행 결과 및 답을 명시하시오.
clear all
clc
f=\'((sin(x)).^3)+((cos(x)).^2)+exp(x)-5\'
n=0; a=0; b=3; err=0.0001;
x=a; fa=eval(f);
x=b; fb=eval(f);
c=b-fb*(a-b)/(fa-fb);
x=c; fc=eval(f);
fprintf(\' L 하한X(l) 상한X(u) 해 오차 \\n\')
while abs(fc)>=err
n=n+1;
x=a; fa=eval(f);
x=b; fb=eval(f);
c=b-fb*(a-b)/(fa-fb);
x=c; fc=eval(f);
if fa*fc<=0
b=c; c=b-fb*(b-a)/(fb-fa);
else
a=c; c=b-fb*(b-a)/(fb-fa);
end
fprintf(\'%5.0f %15.8f %15.8f %15.8f %20.8e \\n\',n, a, b, c, fc)
end
fprintf(\'\\n 총 %2.0f 번 시행하여 나온결과 근사치는 %2.8f 이며, 오차는 %2.8e 입니다. \\n\',n, c, b-c)

































소개글