상호 작용이 있는 액위 시스템 PI/PD 제어기 설계 텀 프로젝트 보고서

소개글

상호 작용이 있는 액위 시스템 PI/PD 제어기 설계 텀 프로젝트 보고서에 대한 보고서 자료입니다.

목차

연구배경
Liquid-level system

1.설계배경
2.설계목표
3.최종 설계 Design
4.설계과정

본문내용

턴스는 단면적과 동일하다. 모든 수두에 대하여 단면적이 일정할 때, 커패시턴스는 일정하다.
변수들의 정의
Q= 정상상태 유량(어떤 변화가 일어나기전),m3/sec
q=정상상태 값으로부터 유입유량의 작은 편차,m3/sec
q1=정상상태 값으로 Tank1에서 Tank2로의 유출유량의 작은편차 m3/sec
q2=정상상태 값으로부터 유출유량의 작은편차,m3/sec
H1,H2=정상상태 수두(어떤 변화가 일어나기전),m
h1,h2=정상상태 값으로부터 수두의 작은편차,m
변수가 정상상태 값으로부터 조금 변한다고 가정하자. 그러면 다음과 같은 식들을 얻을 수 있다.
각 식을 블록선도로 표현한 후 간략화를 계속해서 수행하여 최종 Plant의 전달 함수를 구할 수 있다.
Plant의 최종 전달함수
q를 입력 q2를 출력이라 할 때 시스템의 전달함수는 다음과 같이 나타낼 수 있다.
1.설계배경
시스템 Parameter를 다음과 같이 가정한다.
C1=5m2
C2=3m2
R1=2sec/m2
R2=0.5sec/m2
ess=0.5 (For unit step input)
Plant의 step response로 System의 Dynamics를 알아보았다. 시스템은 oscillation과 Overshoot없어서 상당히 안정화 되어있지만 Settling time(23.7(sec))이 느리다고 판단 하였다. 또한 스텝 입력에 대한 ess도 크다고 판단하였다. Trade-Off를 통하여 Ts를 빠르게 키우고 ess를 줄이기 위해 설계 목표를 다음과 같이 잡았다.
2.설계 목표
1. ess = 0 (For unit step input)
2.
3.
(가능한 4배의 속도상승을 원한다. Ts를 맞추는데 주력, P.O는 약간 손해를 봐도 된다.)
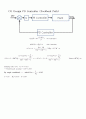
3.최종 설계 Design
4.설계 과정
(1) Design PI Controller(FeedForward Path)
먼저 PI Controller를 사용하여 전체 Closed system 의 ess = 0 으로 맞추도록 한다. 그리고 System의 Transient response 역시 D component를 달기 전 까지 일정수준 정도 맞춰보도록 한다.
(1)Select Zero = -0.5
PI=tf([1,0.5],[1,0])
(2) Damping 0.408 선택 Gain값 0.299
P.O= 25% Ts=76.6(sec)
Transient response 가 너무 요구된 스펙에 못미치게 나왔으므로 Gain값을 올려 보도록 한다.
(3) Damping 0.0973 Gain값 70
P.O=77.3% Ts=18.1(sec)
Settling time은 Speed up 하였으나 P.O와 함께 오실레
이션이 증가하여 System의 특성이 좋지 못하다.
(4)Zero값을 변경하기로 결정 Select Zero = -0.2
PI=tf([1,0.2],[1,0])
변경되어진 Root Locus
(5) damping=0.54 게인값 7.51
P.O= 27.1% Ts=10.1(sec)
(6)Gain값을 9로 잡았을 때 Closed loop System 의 동적 특성
(7)PI 제어기를 달았을 때 System
<=>
Kp=9
z=0.2
Feedforwardpath(S)= 9 s + 1.8
-------------------
15 s^3 + 14 s^2 + s
9 s + 1.8
T(S)= ----------------------------
15 s^3 + 14 s^2 + 10 s + 1.8
P.O=29.3% Ts=8.56(sec)
물론 Step input에 대한 ess = 0이다. Transient response역시 일정수준 맞추어 놓았으므로 D-component를 Feedback 부분에 추가하여 최종적으로 PID제어기를 구성하며 요구하는 Transient response를 맞추도록 한다.
(2) Design PD Controller (Feedback Path) (PI Controller)
(PD Controller)
=0
<=> Where(9=A)
Damping ratio=0.52 Ts=5~7(sec)
=>Desired pole Location= 0.67+1.097i
By angle condition) =>
A=9.36 =0.3577 K=2.907
Closed Loop system의 P-Z map
Pole= -0.673+1.09i,+0.673+1.09i,-0.211
Zero= -0.2
P.O=19% Ts=4.87(sec)
뎀핑을 올려 오버슛을 낮춰 보도록 시도.
A=20 =0.3577 K=6.21
P.O=15.5% Ts=3.21(sec) Ts가 설계 목표에 비해 빠름.
=0.3577 K=2.4
P.O=19.3% Ts=5.5(sec) Settling time만 만족함.
K=8 P.O=13.4% Ts=2.84(sec)
Closed loop system의 P-Z map을 보면 Zero가 0.2에 Pole보다 원점에 있으므로 System을 약간 불안정하게 하여 Overshoot을 줄이는게 어렵다고 판단하였다. -0.2의 Zero는 PI설계에서 나온 Zero이기 때문에 PI제어기의 Zero를 0.2가 아닌 0.6으로 원점으로 멀어지게 설계하여 System을 덜 불안정하게 하도록 해보았다.
=> (Zero값 PI Controller 변경)
Damping ratio=0.56 Ts=6(sec) => Desired Dominent Pole Location=0.67+0.95i
By Angle condition )==> PD제어기의 Zero=1.406 즉 =0.7112
(PD Controller, Feedback Path)
(PI Controller, Feedforward Path)
A==17 K=2.655
Closed Loop System T(S) =
Closed Loop System P-Z Map
Pole= -0.69+0.957i,+0.69+0.957i, -0.687
Zero= 0.6
P.O= 15.3 % 15%
Ts= 5.13(sec)
E(S)=R(S)-Y(S)
S*E(S)=0 <=> =0 (For step input)
Liquid-level system의 설계 목표를 맞추었다.

키워드

자동제어 텀프로젝트,   PID제어기,   PI제어,   PD제어,   PI/PD제어,   액위시스템 설계,   액위시스템 제어기,   제어기 설계,   자동제어 프로젝트