|
주파수보다 더 높은 주파수를 얻기 위해서) - 수정 진동자가 너무 얇으면 기계적으로 약하여 출력이 적기 때문에 01. 우함수,기함수
02. 정적분,부정적분
03. 삼각함수의 정리
04. 무한급수
05. 컨벌루션
06. 함수의 연속성
07. 주기함수
08.
|
|
|
주파수 컨벌루션 정리를 이용하면 다음과 같은 식이 된다.
여기서 이다.
s(t)를 단위 임펄스열로 표본화한 신호 ss(t)의 스펙트럼 는 s(t)의 스펙트럼 의 크기는 로 감소하나 모양은 변하지 않으면서 의 주파수 간격으로 주기 적으로 반복되는 형
|
|
|
주파수 성분을 제거하려면, 를 어떻게 변경하여야 하는지 구하시오.
11. 6-포인트 DFT를 decimation-in-time 기법을 이용하여 2개의 3-포인트 DFT로 분리하여 계산하려 한다. 계산 과정을 FFT와 유사한 흐름도로 그리시오. 이 때, 3-포인트 DFT는 더 이상
|
|
|
컨벌루션은 축 이동이므로 이다. 는 에서 영을 가지고 이므로, , , 이다.
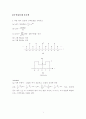
7. 의 스펙트럼이 그림 P4.5일 때, 의 스펙트럼을 구하시오.
그림 P4.5
(solution)
이므로 =이고, 주파수 이동성에 따라 의 스펙트럼은 이다. 또한, 은 마다 반복되므로 이므로
|
|
|
주파수 응답은
H( hat f )= 1 + e^{-j 2 pi hat f } + e^{-j 2 pi 2 hat f }
이므로
H( 1 over 2 )= 1 + e^{-j pi } + e^{-j 2 pi} = 1
이고 출력 신호는
y[n] = (-1) sup n = cos[ pi n]
이 된다.
다른 방법으로, 임펄스 함수와의 컨벌루션 성질을 이용하면
x[n]*y[n] &= x[n] + x[n-1]+x[n-
|
|
메뉴펼치기
