함수 분포

전문지식 491건

	현대물리학 실험 - Maxwell(맥스웰)의 속도분포함수 함수로 나타내었습니다. 플라스틱 모형입자와 철 모형입자를 실험하여 보았지만 위의 식에서도 알 수 있듯이 질량보다는 속도에 우선하기 때문에 분포도 자체에는 그렇게 큰 영향을 미치지 못함을 알 수 있었습니다. 이번 실험을 통해서 Max 현대물리학 실험 속도분포함수, Maxwell(맥스웰) Maxwell(맥스웰)의 속도분포함수, 현대물리학 실험 - Maxwell(맥스웰)의 속도분포함수,	페이지 7페이지 가격 1,800원 등록일 2014.05.20 파일종류 한글(hwp) 참고문헌 있음 최근 2주 판매 이력 없음
	경영통계학]?이산확률분포와?연속확률분포를?정의한?후,?두?확률분포의?차이점을?... 분포는 이산적인 값을 가지며 확률값은 유한하거나 자연수만큼만 존재합니다. 예를 들어, 동전 던지기에서 앞면과 뒷면이 각각 1/2의 확률로 발생한다면, 확률변수 X의 값은 0 또는 1이 됩니다. 이러한 이산적인 값이 확률밀도함수를 통해 나타 경영통계학, 이산확률분포, 연속확률분포, 경영통계학 이산확률분포, 경영통계학]?이산확률분포와?연속확률분포를?정의한?후,?두?확률분포의?차이점을?사례를?들어?설명하시,	페이지 11페이지 가격 2,000원 등록일 2023.07.01 파일종류 아크로벳(pdf) 참고문헌 있음 최근 2주 판매 이력 없음
	경영통계학 ) 연속확률분포에 대하여 요약하여 정리하시오 함수도 이야기를 하겠다. 연속확률변수는 이렇게 특정한 확률변수 값의 확률을 정의할 수 없어서 연속확률변수의 누적분포함수를 구하기 위해선 lim라는 극한값의 방법을 이용하게 된다. 그럼 확률밀도 함수의 성질도 정리해보도록 하겠다. 1 연속, 활률, 분포, 연속 활률, 경영통계학 ) 연속확률분포에 대하여 요약하여 정리하시오,	페이지 6페이지 가격 3,700원 등록일 2023.02.17 파일종류 한글(hwp) 참고문헌 있음 최근 2주 판매 이력 없음
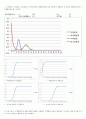
	[레포트자료] 이항분포, 기하분포, 초기하분포, 푸아송분포(푸아종분포)의 확률밀... V(x)=30 V(x)=np= 100x0.3=30 3.이항분포, 초기하분포, 푸아송분포의 엑셀함수를 이용하여 그려보고 문제 2에서 함수식을 이용하여 그린 분포와 비교하라. 이항분포 엑셀함수 분포 이항분포 함수식 이용 분포 기하분포 엑셀함수 분포 기하분포 함수식 이항분포 초기하분포, 기하분포 확률밀도함수식, [레포트자료] 이항분포, 기하분포, 초기하분포, 푸아송분포(푸아종분포)의 확률밀도함수식,	페이지 3페이지 가격 8,400원 등록일 2015.05.09 파일종류 한글(hwp) 참고문헌 없음 최근 2주 판매 이력 없음
	이항분포의 정리 입력(ctrl+shift+enter)하면 에러없이 정상적으로 값이 출력되는 것을 볼 수 있다. 1)이산확률분포(discrete probability distribution)의 정의 2)이항분포의 정의 3)이항분포의 확률밀도함수 4)이항분포의 특성치 5)이항 분포 함수 6)예제 이항분포 확률밀도함수, 이산확률분포 이항분포함수, 이항분포의 정리,	페이지 5페이지 가격 800원 등록일 2002.10.29 파일종류 한글(hwp) 참고문헌 없음 최근 2주 판매 이력 없음