목차
7. 대수논리와 드모르간 정리, 간소화
∎ 실험목적
∎ 실험부품 및 사용기기
∎ 이론요약
∎ 실험순서
7. 대수논리와 드모르간 정리, 간소화
∎ 실험목적
∎ 실험부품 및 사용기기
∎ 이론요약
∎ 실험순서
∎ 실험목적
∎ 실험부품 및 사용기기
∎ 이론요약
∎ 실험순서
7. 대수논리와 드모르간 정리, 간소화
∎ 실험목적
∎ 실험부품 및 사용기기
∎ 이론요약
∎ 실험순서
본문내용
0일때와 B가 1일때의 를 측정하자.
B=0일때
B=1
⑥ logic equation11을 만족하는 회로를 구성한 후 B가 0 또는 1일때의 입력과 출력의 전압을 측정하자.
B=0일때
B=1일때
8. 논리회로 간소화
실험목적
BCD - 부당한 코드 탐지기의 진리표를 나타낸다.
논리식을 간략화 하기 위해서 카르노맵(Karnaugh-map)을 이용한다.
간략화 된 논리식을 실행하는 회로를 설계하고 실험한다.
실험부품 및 사용기기
7400 NAND 게이트
LED
DIP 스위치
브레드 보드
5V 직류전압전원 장치
DMM
저항기 330Ω, 1kΩ
이론요약
조합 논리 회로들의 출력은 입력에 의해서만 결정되어진다. 간단한 조합 회로의 경우, 진리표가 모든 가능한 입력과 출력을 대응시키는데 사용되어진다. 진리표는 회로에서 원하는 동작을 완벽하게 표현한다. 그 회로는 진리표에서 읽은 출력 함수에 대한 표현식을 간소화함으로써 구현되어진다.
Input
Output
X
0 0
0 0
1
0 0
0 1
0
0 0
1 0
0
0 0
1 1
0
0 1
0 0
1
0 1
0 1
1
0 1
1 0
0
0 1
1 1
0
1 0
0 0
1
1 0
0 1
1
1 0
1 0
1
1 0
1 1
0
1 1
0 0
1
1 1
0 1
1
1 1
1 0
1
1 1
1 1
1
조합 논리 회로의 간소화에 널리 쓰이는 기술을 M. Karnaugh에 의해서 개발되었다. 이 방법은 인접한 셀에서는 각각이 단 하나의 변수만 서로 다른 기하학적인 맵에 진리표를 써넣는 것이다.(인접한 셀은 공동 수직 또는 공동 수평으로 같은 경계를 포함한다.) 카노맵을 그릴 때, 변수들은 맵의 옆면과 맨 위에서부터 그레이코드 순열로 쓰여진다. 맵 위의 각 셀은 진리표의 한 행과 대응된다. 출력 변수는 주어진 진리표의 대응된 위치에 ‘0’과 ‘1’로 나타난다. 예로써 2비트 비교기의 설계를 생각해 본다. 입력은 과 으로 한다. 만약 이 과 같거나 더 크면 출력은 HIGH가 된다. 표 8-1에 제시된 대로 원하는 출력을 진리표로 쓴 후에 시작한다. 모든 가능한 입력은 진리표에 의해 분명하게 제시되어 지고 원하는 출력은 모든 가능한 입력에 대해 주어진다.
다음에 그림 8-1에 제시된 대로, 카노맵을 그린다. 이 예에서 맵은 숫자를 사용하여 입력을 표시했다. 맵에서 셀들의 인접 셀을 묶음으로써 곱의합(SOP)형태로 해석될 수 있다. 그룹의 크기는 2의 거듭 제곱(1,2,4,8 등등)이어야 하고 가능한 가장 큰 그룹을 선택한다. 모든 1셀이 최소한 하나의 그룹에 속해 있어야만 하고, 필요하다면 하나 이상의 그룹으로 묶는다.
각 그룹은 간소화된 출력 함수에서 하나의 곱의 항으로 해석된다. 독립적인 1셀 보다 큰 각 그룹내에서는 출력 표현식에서 변수가 소거될 수 있도록 하기 위해 인접한 경계는 교차되어 있다. 인접한 1셀이 2개인 그룹(pair)은 하나의 인접 경계를 가지게 되고, 하나의 변수가 소거되어진다. 1셀이 4개인 그룹(quad)은 두 개의 변수가 소거되어지고, 1이 8개인 그룹(octet)은 세 개의 변수가 소거된다. 그림 8-1은 2비트 비교기의 카노맵에서 그룹으로 만드는 방법을 나타낸다. 이 경우에 각 그룹은 네 개의 1셀이 하나의 그룹이기 때문에 각 곱의 항은 두 변수를 포함한다.(두 변수는 각 항에서 소거되어졌다.)
실험순서
이번 실험에서는 계수기와 제어 시스템의 확장으로서, 단지 유효한 BCD코드가 레지스터 A에 표시되도록 보장하고, 만약 부당한 BCD 코드가 발견되면 경보 신호를 발생하는 회로를 설계한다. 회로는 4비트로 설계하지만, 레지스터 A에 대해 8비트로 확장이 간단히 된다. 그림 8-3은 부당한 코드 탐지하는 시스템이다. BCD는 0에서 9까지의 10진수를 나타내는 4비트 2진 코드이고, 2진수 1010에서 1111까지가 BCD에서는 부당한 값이 된다.
1. 보고서의 표 8-2에 제시된 진리표를 완성한다. 10개의 유효 BCD 코드의 출력은 0으로 6개의 부당한 BCD 코드의 출력은 1로 가정한다. 숫자 표시기에 사용되듯이 MSB는 문자 D로 표시되고 LSB는 문자 A로 표시되어진다.
2. 보고서의 그림 8-4에 제시된 카노맵을 완성한다. 이론 요약에서 설명한대로 1셀을 그룹으로 만든다. 맵에서 최소 곱의 합(SOP)을 묶음으로써 부당한 코드 표현식을 찾아낸다. 보고서의 준비된 여백에 간소화된 논리식을 쓴다.
3. 과정 2의 논리식을 정확하게 썼다면, 곱의 항이 두 개이고 문자 D가 두 항 모두에 나타나게 된다. 이 논리식은 완전한 논리 회로로 수행되어진다. 각 항에서 D를 인수분해 하면, 부당한 코드의 다른 논리식을 얻게 된다. 보고서의 준비된 여백에 새로운 논리식을 쓴다.
4. TTL 논리를 다시 생각해 보면, LOW는 의 한계를 벗어나지 않고 LED를 켜지게 할 수 있다. 그러나 HIGH는 의 한계를 초과하게 된다. 이것을 피하기 위해 출력은 역으로 되고 가 LOW 논리 레벨에서 LED를 켜지도록 사용되어 진다. 그림 8-5에 과정 3의 논리식을 수행하는 회로가 제시되어 있다.
5. 그림 8-5에 제시된 회로가 단지 두 개의 게이트만으로 설계에 필요한 것을 충족시키지만, 그것은 두 가지의 다른 IC를 필요로 한다. 어떤 경우에 있어서는 이것이 최고의 설계가 될 수 있다. 그러나 NAND 게이트의 일반적인 특성을 이용해서 OR게이트는 세 개의 NAND 게이트의 일반적인 특성을 이용해서 OR게이트는 세 개의 NAND 게이트로 대치함으로써 그 회로가 단 하나의 IC 7400으로 실행되도록 한다. OR 게이트를 세 개의 NAND 게이트로 대치시켜서 그림 8-5의 회로를 변환시킨다. 보고서의 준비된 여백에 새로운 회로를 그린다.
6. 과정 5에서 그린 회로를 구성한다. 모든 입력 조합을 검사하고 보고서의 진리표 8-3을 완성한다. 만약 회로를 정확하게 구성하고 실험했다면, 그 진리표는 표 8-2와 같다.
입력이 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001일 경우
·입력이 1010, 1011, 1100, 1101, 1110, 1111일 경우
B=0일때
B=1
⑥ logic equation11을 만족하는 회로를 구성한 후 B가 0 또는 1일때의 입력과 출력의 전압을 측정하자.
B=0일때
B=1일때
8. 논리회로 간소화
실험목적
BCD - 부당한 코드 탐지기의 진리표를 나타낸다.
논리식을 간략화 하기 위해서 카르노맵(Karnaugh-map)을 이용한다.
간략화 된 논리식을 실행하는 회로를 설계하고 실험한다.
실험부품 및 사용기기
7400 NAND 게이트
LED
DIP 스위치
브레드 보드
5V 직류전압전원 장치
DMM
저항기 330Ω, 1kΩ
이론요약
조합 논리 회로들의 출력은 입력에 의해서만 결정되어진다. 간단한 조합 회로의 경우, 진리표가 모든 가능한 입력과 출력을 대응시키는데 사용되어진다. 진리표는 회로에서 원하는 동작을 완벽하게 표현한다. 그 회로는 진리표에서 읽은 출력 함수에 대한 표현식을 간소화함으로써 구현되어진다.
Input
Output
X
0 0
0 0
1
0 0
0 1
0
0 0
1 0
0
0 0
1 1
0
0 1
0 0
1
0 1
0 1
1
0 1
1 0
0
0 1
1 1
0
1 0
0 0
1
1 0
0 1
1
1 0
1 0
1
1 0
1 1
0
1 1
0 0
1
1 1
0 1
1
1 1
1 0
1
1 1
1 1
1
조합 논리 회로의 간소화에 널리 쓰이는 기술을 M. Karnaugh에 의해서 개발되었다. 이 방법은 인접한 셀에서는 각각이 단 하나의 변수만 서로 다른 기하학적인 맵에 진리표를 써넣는 것이다.(인접한 셀은 공동 수직 또는 공동 수평으로 같은 경계를 포함한다.) 카노맵을 그릴 때, 변수들은 맵의 옆면과 맨 위에서부터 그레이코드 순열로 쓰여진다. 맵 위의 각 셀은 진리표의 한 행과 대응된다. 출력 변수는 주어진 진리표의 대응된 위치에 ‘0’과 ‘1’로 나타난다. 예로써 2비트 비교기의 설계를 생각해 본다. 입력은 과 으로 한다. 만약 이 과 같거나 더 크면 출력은 HIGH가 된다. 표 8-1에 제시된 대로 원하는 출력을 진리표로 쓴 후에 시작한다. 모든 가능한 입력은 진리표에 의해 분명하게 제시되어 지고 원하는 출력은 모든 가능한 입력에 대해 주어진다.
다음에 그림 8-1에 제시된 대로, 카노맵을 그린다. 이 예에서 맵은 숫자를 사용하여 입력을 표시했다. 맵에서 셀들의 인접 셀을 묶음으로써 곱의합(SOP)형태로 해석될 수 있다. 그룹의 크기는 2의 거듭 제곱(1,2,4,8 등등)이어야 하고 가능한 가장 큰 그룹을 선택한다. 모든 1셀이 최소한 하나의 그룹에 속해 있어야만 하고, 필요하다면 하나 이상의 그룹으로 묶는다.
각 그룹은 간소화된 출력 함수에서 하나의 곱의 항으로 해석된다. 독립적인 1셀 보다 큰 각 그룹내에서는 출력 표현식에서 변수가 소거될 수 있도록 하기 위해 인접한 경계는 교차되어 있다. 인접한 1셀이 2개인 그룹(pair)은 하나의 인접 경계를 가지게 되고, 하나의 변수가 소거되어진다. 1셀이 4개인 그룹(quad)은 두 개의 변수가 소거되어지고, 1이 8개인 그룹(octet)은 세 개의 변수가 소거된다. 그림 8-1은 2비트 비교기의 카노맵에서 그룹으로 만드는 방법을 나타낸다. 이 경우에 각 그룹은 네 개의 1셀이 하나의 그룹이기 때문에 각 곱의 항은 두 변수를 포함한다.(두 변수는 각 항에서 소거되어졌다.)
실험순서
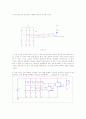
이번 실험에서는 계수기와 제어 시스템의 확장으로서, 단지 유효한 BCD코드가 레지스터 A에 표시되도록 보장하고, 만약 부당한 BCD 코드가 발견되면 경보 신호를 발생하는 회로를 설계한다. 회로는 4비트로 설계하지만, 레지스터 A에 대해 8비트로 확장이 간단히 된다. 그림 8-3은 부당한 코드 탐지하는 시스템이다. BCD는 0에서 9까지의 10진수를 나타내는 4비트 2진 코드이고, 2진수 1010에서 1111까지가 BCD에서는 부당한 값이 된다.
1. 보고서의 표 8-2에 제시된 진리표를 완성한다. 10개의 유효 BCD 코드의 출력은 0으로 6개의 부당한 BCD 코드의 출력은 1로 가정한다. 숫자 표시기에 사용되듯이 MSB는 문자 D로 표시되고 LSB는 문자 A로 표시되어진다.
2. 보고서의 그림 8-4에 제시된 카노맵을 완성한다. 이론 요약에서 설명한대로 1셀을 그룹으로 만든다. 맵에서 최소 곱의 합(SOP)을 묶음으로써 부당한 코드 표현식을 찾아낸다. 보고서의 준비된 여백에 간소화된 논리식을 쓴다.
3. 과정 2의 논리식을 정확하게 썼다면, 곱의 항이 두 개이고 문자 D가 두 항 모두에 나타나게 된다. 이 논리식은 완전한 논리 회로로 수행되어진다. 각 항에서 D를 인수분해 하면, 부당한 코드의 다른 논리식을 얻게 된다. 보고서의 준비된 여백에 새로운 논리식을 쓴다.
4. TTL 논리를 다시 생각해 보면, LOW는 의 한계를 벗어나지 않고 LED를 켜지게 할 수 있다. 그러나 HIGH는 의 한계를 초과하게 된다. 이것을 피하기 위해 출력은 역으로 되고 가 LOW 논리 레벨에서 LED를 켜지도록 사용되어 진다. 그림 8-5에 과정 3의 논리식을 수행하는 회로가 제시되어 있다.
5. 그림 8-5에 제시된 회로가 단지 두 개의 게이트만으로 설계에 필요한 것을 충족시키지만, 그것은 두 가지의 다른 IC를 필요로 한다. 어떤 경우에 있어서는 이것이 최고의 설계가 될 수 있다. 그러나 NAND 게이트의 일반적인 특성을 이용해서 OR게이트는 세 개의 NAND 게이트의 일반적인 특성을 이용해서 OR게이트는 세 개의 NAND 게이트로 대치함으로써 그 회로가 단 하나의 IC 7400으로 실행되도록 한다. OR 게이트를 세 개의 NAND 게이트로 대치시켜서 그림 8-5의 회로를 변환시킨다. 보고서의 준비된 여백에 새로운 회로를 그린다.
6. 과정 5에서 그린 회로를 구성한다. 모든 입력 조합을 검사하고 보고서의 진리표 8-3을 완성한다. 만약 회로를 정확하게 구성하고 실험했다면, 그 진리표는 표 8-2와 같다.
입력이 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001일 경우
·입력이 1010, 1011, 1100, 1101, 1110, 1111일 경우
































소개글