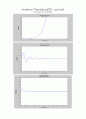
|
Solution to the Inverted Pendulum Problem Using LQR design
* x=1, y=1
* x=5000, y=100
*x=4500, y=100
*x=5000, y=200 * x=1, y=1
* x=5000, y=100
*x=4500, y=100
*x=5000, y=200
|
|
|
LQR control)
M = 2;
m = 0.1;
g = 9.8;
l = 0.5;
p = M*m*l^2; %denominator
A = [0 1 0 0;
0 0 (m^2*g*l^2)/p 0;
0 0 0 1;
0 0 m*g*l*(M+m)/p 0];
B = [0; (m*l^2)/p; 0; m*l/p];
C = [1 0 0 0;
0 0 1 0];
D = [0;0];
x=1;
y=1;
Q=[x 0 0 0;
0 0 0 0;
0 0 y 0;
0 0 0 0];
R = 1;
K = lqr(A,B,Q,R)
Ac = [(A-B*K)];
Bc = [
|
|
|
매트랩의 lqr(), lqe()함수를 이용하여 Try & Error 방식으로 위의 설계제한조건에 맞는 값을 찾으려고 하였다. 값이 크게 되면 정착시간이 빨라지지만 그만큼 오버슈트가 크게 생기고 작으면 그 반대의 상황이 발생한다. 그리고 q값이 크게 되면 시
|
|
메뉴펼치기
