|
맥스웰-볼츠만 분포의 개념을 금융시장에 어떻게 적용할 수 있는지 설명하고,
이를 통해 시장 참여자의 심리 상태를 분석하며,
온도(거래량, 변동성)의 높고 낮음에 따라 적절한 매매전략이 어떻게 달라지는지 구체적으로 제시하는 것입니
|
|
|
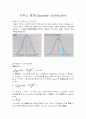
분포. 이 확률을 나타내는 법칙은 1859년에 J.C. 맥스웰이 속도분포법칙으로 제출하였고, 그 후 68년에 L. 볼츠만이 일반화하였다. 같은 종류인 개의 분자로 이루어지고 상호작용을 갖지 않는 기체가 퍼텐셜을 갖는 외력의 장내에 있고 절대온도
|
|
|
분포는 입자들 사이의 충돌에 의해서 평형에 도달하게 되는데 그것을 통계낸 것이 맥스웰-볼츠만 분포 Maxwell-Boltzmann distribution 다. 이 분포도에서 평형으로 접근하는 동안에 볼츠만의 함수는 감소하고, 평형상태, 즉 최소값을 갖게 되면, 충돌
|
|
|
맥스웰-볼츠만 분포, 입자속도의 확률분포)
자의식이 세포의 내적인 움직임이라 하는 것이 신경학의 입장이지만 사실 자의식과 같은 현상이 일어나기에 세포의 구조는 너무 거시적이라 한다. 양자적 요동이 자의식을 만든다는 해석이 있다.
|
|
|
분포식과 Fermi function에 의하여 다음 그림과 같이 나타낼 수 있다.
T=0인 상태에서 다음과 같은 근사식을 쓸 수 있다.
Ef = Ef0[1-(π2/12)(kT/Ef0)2] (식11)
금속의 경우는 Ef0는 수 eV이므로 kT/Ef0 ≪ 1
∴EfEf0 이상기체의 맥스웰-볼쯔만 분포
Fermi-dirac
|
|
 |
분포에 대하여 설명해보세요.
32
msds란 무엇인가요?
33
기존 직장에서 가장 잘못했던 사례와 해결책은 무엇인가요?
34
맥스웰 방정식에 대해 설명해보시오.
35
중대재해처벌법에 관한 자신의 견해를 말해주세요.
36
안전이 뭐라고 생각하는지?
37
|
|
메뉴펼치기
