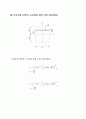
|
직사각형 단면의 도심축에 관한 단면 2차모멘트
직사각형 단면의 도심축에 관한 단면 2차모멘트는.
삼각형 단면의 도심축(X축)에 관한 단면 2차모멘트
삼각형의 도심축에 관한 단면2차모멘트
기울기 :
먼저, 밑면에 대한 단면2차모멘트는
만
|
|
|
원의 단면2차 모멘트는 다음과 같다.
여기서 은 원의 반지름이다. 원의 경우에는 모든 방향의 도심축에 대해 단면 2차 모멘트가 동일하다. 도심축이 중심과 일치하는 경우, 반지름 방향으로 각 요소의 면적에 대해 아래와 같이 적분할 수 있다.
|
|
|
다. x는 중심축과 수직인 좌표축이다.
이중 적분을 해서 단면 2차 모멘트를 구하면 다음과 같다.
위와 같은 방식으로, 도심축이 세로축과 일치하는 경우의 단면 2차 모멘트를 구할 수 있다.
이중 적분을 해서 단면 2차 모멘트를 구하면 다음과
|
|
|
단면 : 도심의 두 대칭축( x,y )의 교점에 있다.
- 1축 대칭단면 : 대칭축상에 있다.
․도심구하기(1축 대칭단면)
≪ 그 림 ≫ ≪ 그 림 ≫
그림 [a] 그림 [b]
≪ … 중 략 … ≫
1.3 단면2차모멘트(Moment of inertia)
|
|
|
단면2차 모멘트 I =
이 이론식을 가지고 데이터값과 비교 할 수 있다.
<데이터값>
하중(N)
스팬길이(mm)
처짐량(mm)-1차
처짐량(mm)-2차
처짐량(mm)-평균값
스팬길이(L^3)
E(탄성계수)-205kN
I(극2차모멘트)-(25*5^3)/12
처짐량-이론값(WL^3)/(48EI)
50
1000
19.3
|
|
 |
단면2차모멘트
==기초의 y축에 대한 단면2차모멘트
=x축에 대한 기둥하중에 의한 모멘트 =
=y축에 대한 기둥하중에 의한 모멘트 =
=x방향으로의 하중 편심거리
=y방향으로의 하중 편심거리
,는 ,축을 사용해서 다음과 같이 구한다.
7.얕은 기초의
|
|
|
단면의 분류
3.2 보의 횡좌굴 응력과 허용휨응력
3.3 보의 구멍 뚫림
3.4 보의 처짐
3.5 형강보의 설계
제 4 장 수계산에 의한 부재해석
4.1 격점 하중의 분담력 계산
제 5 장 전산해석
5.1 마이다스를 활용한 부재해석
5.2 네오맥스를
|
|
 |
모멘트에 대해서 말해주세요.
23
공정안전보고서가 무엇인가요?
24
제품의 물성을 조절하기 위해 어떤 공정을 선택할 것이며 그 이유는 무엇인가요?
25
pid제어기 원리는 무엇인가요?
26
강도와 전기전도도를 동시에 올리려면 어떻게 되나요?
27
|
|
메뉴펼치기
