|
법>
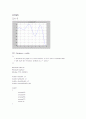
<뉴턴법> - (x가 0일 때 미분계수가 0이되어 뉴턴법을 쓸수 없으므로 초기 x값은 1로 정하였다.)
<할선법>
이분법
뉴턴법
할선법
계산횟수
14
4
7
x값
0.617980957
0.618033995
0.618033988
오차
0.000061035
0.000076702
0.000001465
5. 결과 분석
<이분
|
|
|
f(double x)
{
return((-32.17/(2*pow(x,2)))*((pow(2.718281828,x)-pow(2.718281828,-x))/2-sin(x))-1.7);
} 1. 서론
2. 본론
1) 이분법
2) 할선법
3) 가위치법
4) 뉴튼-랩슨법
5) Aitken 델타제곱법
6) 뮬러
3. 결론
4. 별지
5. 소스 및 결과
|
|
|
6<0
f(2)*f(2.7)=(-1)*0.4=-0.4<0
f(2)*f(2.6)=(-1)*0.2=-0.2<0
f(2)*f(2.5)=(-1)*0=0이므로
따라서 f(x)=2x-5의 근 x=2.5이다.
●참고자료
-http://100.naver.com/100.nhn?docid=40667
-http://kr.blog.yahoo.com/sumloss/97806
|
|
|
%f\n",p2);
while(absol(p2-p1)>=TOL)
{
p1 = p2;
p2 = p1 - f(p1)/fp(p1);
n++;
printf("n= %d Pn= %f f(Pn)= %f \n",n,p2,f(p2));
}
printf("Solution is %f\n\n",p2);
return 0;
}
(2)Result
HW#7
2.4-9
(1) Source code
/*
I sketched the graph of f(x)=x^2 -3 and I concluded that
I will start the Newton's m
|
|
|
Newton-Raphson 법을 사용하라.
(세 번 반복계산하고, 초기 가정값은 x_i = 3.5를 사용하라)
⒞ 할선법을 사용하라.
(세 번 반복계산하고, 초기 가정값은 x_i-1 = 2.5 와 x_i = 3.5를 사용하라)
⒟ 수정된 할선법을 사용하라.
(세 번 반복계산하고, 초기 가정
|
|
 |
법 입법 예고안(환경부 2003. 12.30)
<표2-2> 공중위생관리법 기준(보건복지부)
<표2-3> 후생노동성 지침치
<표2-4> 빌딩위생관리법 규제 기준(후생노동성, 2003.4.1 확대 개정시행)
<표2-5> 환경보호청(미국EPA)가이드 라인
<표2-6> 캐나다 Health Canada 가
|
|
 |
법칙에 대해 설명하고 예를 들어 보세요.
23. 뉴턴의 3가지 법칙에 대하여 말해 보세요.
24. 결정에 대해 아는 것을 설명해주세요.
25. 농축이란 무엇인가요?
26. 흡착이란 무엇인가요?
27. 비열이란 무엇인가요?
28. 흡착이란 무엇인가요?
29.
|
|
 |
뉴튼의 운동법칙
수퍼기어와 헬리컬 기어
고유진동수와 강제진동
열간가공과 냉간가공
응력-변형률선도
최적의 설계
소성가공의 종류 현대다이모스자소서 현대다이모스 생산직 자기소개서 R&D 자소서,현대다이모스 생산지원 자소서,현
|
|
메뉴펼치기
