|
Fourier 급수의 값은 으로 수렴합니다.
간단히 말해서, 두 점의 평균값으로 수렴하는 것입니다.
※적분 변환의 정의
푸리에 변환과 라플라스 변환은 모두 적분 변환의 일종이다. 적분 변환은 \"적분을 이용하여 함수를 함수로 옮기는 사항\"입니
|
|
|
변환의 쓰임새와 상호관계
4-1 각 변환의 쓰임새
푸리에급수 : 연속적인 주기 신호의 주파수 영역의 신호해석을 할 때 사용
푸리에변환 : 연속적인 비주기 신호의 주파수 영역의 신호해석을 할 때 사용
(시스템과 신호가 모두 안정한 경우에만
|
|
|
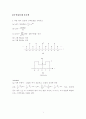
푸리에 급수 계수를 라 한다.
4. 가 그림 P4.4의 스펙트럼을 가질 때, 의 스펙트럼을 그리시오.
5. 다음 값을 구하시오
6. 이다. 의 스펙트럼을 라 할 때, 에서의 값을 각각 구하시오.
7. 의 스펙트럼이 그림 P4.5일 때, 의 스펙트럼을 구하시
|
|
|
변환의 중요 공식 정리
선형성의 정리
시간 추이 정리
복소 추이 정리
복소 미분 정리
초기값 정리
최종값 정리
13. 전달 함수
1) 각종 요소의 전달함수
전달함수는 모든 초기 조건을 0으로 했을 경우 입력에 대한 출력의 비를 말한다.
순위
요소
|
|
|
급수적으로 감소한다.
진동 에너지 준위 E₁에 있는 분자의 수 N₁은 바닥 상태(기저 상태)의 분자 수 N에 대해 다음과 같이 표현된다.
N₁ = N × exp[(E₁ E)/(kT)]
여기서 k는 볼츠만 상수이며, T는 절대 온도이다. 일반적으로 진동 준위 간의 에너
|
|
 |
2.문학 속의 로봇이야기
(1)생각하는 로봇
(2)탑승 로봇
(3)사이보그
3.실현 가능성
Ⅲ. 생명문학
1.생명문학의 기원
2.문학 속의 생명이야기
(1)생체 강화
(2)생체 변환
3.실현 가능성
Ⅳ. 결론
|
|
|
급수한다.
② 습윤양생 기간은 반드시 3일 이상이어야 한다.
③ 직사광과 바람을 막기위해 양생포로 받침을 밀봉한다.
* 동절기
① 양생온도 저하를 막고 타설부위의 적절한 보온 조치를 통하여 수화반응이 원활하게 되도록 하여야 하며 발
|
|
|
최종적으로 = 의 상태로 제어계의 밸런스가 잡혀 모터를 정속으로 회전시킬 수 있다. 또한 이 제어계에서 타코-제네레이터를 주파수 발생기 FG로 변환하고 제어에 의한 정속제어 회로를 만들 수 있다(그림2-8(b)). 또 기준전압 발생부를 수정발
|
|
 |
푸리에 급수한?
10. 전압변동률이란?
11. 과도현상이란?
12. 풍력발전소의 조건은?
13. 살면서 가장 힘들었던 경험을 말해보라.
14. 노조에 대해 어떻게 생각하는가?
15. 입사하면 어떤 일을 하고 싶은가?
16. 당사에 대해 아는대로 말해보라.
17. 10년
|
|
 |
푸리에 급수란?
풍력발전소의 조건은?
전력시장에 대해 설명해보라.
전기 품질 요소에 대해 말해보라.
남한과 북한의 송전선로 건설 시 어떤 변화가 있겠는가?
우리나라 주파수 정격은?
과도 현상이란? 1. 본인이 맡은 일에 대하여 주인의
|
|
 |
푸리에 급수란?
풍력발전소의 조건은?
전력시장에 대해 설명해보라.
전기 품질 요소에 대해 말해보라.
남한과 북한의 송전선로 건설 시 어떤 변화가 있겠는가?
우리나라 주파수 정격은?
과도 현상이란? < 자소서 항목 >
1. 완수하기 어려
|
|
 |
푸리에 급수란?
풍력발전소의 조건은?
전력시장에 대해 설명해보라.
전기 품질 요소에 대해 말해보라.
남한과 북한의 송전선로 건설 시 어떤 변화가 있겠는가?
우리나라 주파수 정격은?
과도 현상이란? 1. 자기소개 (성격의 장단점 포함) [10
|
|
 |
푸리에 급수란?
풍력발전소의 조건은?
전력시장에 대해 설명해보라.
전기 품질 요소에 대해 말해보라.
남한과 북한의 송전선로 건설 시 어떤 변화가 있겠는가?
우리나라 주파수 정격은?
과도 현상이란? 1. 자기소개 (성격의 장단점 포함) [10
|
|
메뉴펼치기
