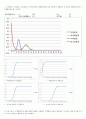
|
이항분포와 푸아종분포의 분포도는 비슷해짐을 알 수 있다. 1. 이항분포, 기하분포, 초기하분포, 푸아송분포의 확률밀도함수식을 이용하여 엑셀에서 각 분포의 확률분포도와 누적확률분포도를 그리시오.
2. 문제 1에서 각 확률변수에 대
|
|
|
입력(ctrl+shift+enter)하면 에러없이 정상적으로 값이 출력되는 것을 볼 수 있다. 1)이산확률분포(discrete probability distribution)의 정의
2)이항분포의 정의
3)이항분포의 확률밀도함수
4)이항분포의 특성치
5)이항 분포 함수
6)예제
|
|
|
확률계산에서는 소수점 이하 계산이 많다. 반올림은 일반적으로 소숫점 이하 세 자리에서 하나 유효수치가 적어도 셋은 되도록 한다. 1)정의
2)포아송 분포의 확률밀도함수
3)포아송분포의 특성치
4)이항분포와 포아송분포의 관계
|
|
|
분포의 관계
이항분포(p≤0.5, np≥5) =>
↓(p≤0.1, n≥50) [정규분포N(np, npq)]
포아송분포(np≥5) =====>
3. 표준정규분포 : 정규 확률변수의 표준화 ⇒ 확률밀도함수
#. 표준정규분포표 보는 방법 : 표 內의 값은 확
|
|
|
분포로 근접할 수 있다. 하지만 반대로 가우시안을 PMF로 나타낼 수 는 없다. 또한 PMF가 가우시안 분포로 접근하기는 하나 PMF는 결국 임펄스 파형이므로 완벽히 가우시안 분포와 같을 수 없다. X를 이항분포 에 따르는 PMF 함수의 평균은 , 분산
|
|
메뉴펼치기
