|
nt response에 별다른 영향을 미치지 않는다.
그러나 이 pole이 steady-state error 보상해준다.
2. 이론값과 실험값의 차이에 대하여 토의하시오.
이유 중 하나로 Op Amp가 이상적인 조건이 아닌 증폭률 A를 가지고 있기 때문이다. 만약 증폭률이 큰 비싼
|
|
|
pole과 zero가 많아 위상각이 많이 떨어지는 것을 확인할 수 있었다. 때문에 시스템의 안정도에 있어서 Resonator회로로 만든 filter가 더 안정하다고 판단할 수 있다.
설계 3. OP-AMP-RC FILTER은 OP-AMP와 R,C를 이용하여 주요 3가지 여파기(Resonator 회로와 KH
|
|
|
안정도를 결정 할 수 있다. 전달함수의 pole, zero, steady state error 등의 값을 이용하여 시스템을 안정적으로 만들 수 있는 controller를 선택하여야 한다. 시스템이 불안정한 상태로 가게 되면, 오작동 뿐 아니라 큰 사고도 유발할 수 있다. 3가지 contr
|
|
|
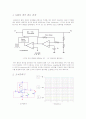
안정도를 평가하기 위해 전달함수 의 극점과 영점을 구할 필요가 있다.
이 함수의 크기는 로 갈 때 영(Zero)로 접근한다.
그러므로, 일 때 는 0이라고 말할 수 있다.
이 함수는 일 때 무한대로 접근하므로 는 일 때 극점(pole)을 가진다고 말할 수
|
|
|
poles);
poles2 = [0 0];
Lt = acker(P',C',poles2);
L=Lt';
Pnew = [P-G*K zeros(size(A));L*C-G*K P-L*C];
Gnew = [G;zeros(size(G))];
Cnew = [C zeros(size(C))];
SYS = ss(Pnew,Gnew,Cnew,D);
SYSD=c2d(SYS,1,'zoh');
step(SYSD)
-Root Locus-
8.21-(a),(b) 시뮬레이션
-소스코드-
clear
G = tf([1],[1 1 0]);
K = 2.0
|
|
 |
안정도 향상, 신재생변동성 및 발전제약 완화)- 직류송전 (HVDC, 장거리 송전, 국가간 전력네트워크 구성)- 유연송전 (FACTS, 반도체 소자 활용 전력계통 고속제어)- 고효율 송전 (초전도, 저항 zero, 손실절감, 꿈의 기술 상용화)- IoT 빅데이터 광역
|
|
메뉴펼치기
