|
Gate - AND, OR, NOT
Complex Gate - NAND, NOR, XOR, XNOR
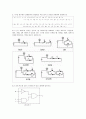
2.14 다이오드와 저항을 이용하여 정 논리(positive logic)의 AND 게이트 및 OR 게이트 회로를 각각 그리고, 각각의 입출력 전압 전달 특성표와 진리표를 작성하시오.
A
B
F
0
0
0
0
1
0
1
0
0
1
1
1
AND
A
B
F
0V
0V
0V
0V
5
|
|
|
OR한 다음 부정한 것은 두 신호를 각각 부정한 다음 AND한 것과 같다"는 것을 알 수 있다. 위의 항등식을 다음 진리표를 이용하여 증명해 본다 1. 실험목적
2. 실험이론
(1)NAND 게이트의 변환
(2) NOB 게이트의 변환
3. 실험방법
예비고찰
|
|
|
AND gate는
입력단자의 여러가지 조합에 대하여 논리곱과 동일한 결과를 출력하는 소자. 실험2. 게이트와 부울대수 및 조합논리 회로
AND - Gate
OR - Gate
NOT - Gate
NAND - Gate
NOR - Gate
Exclusive-OR - Gate
Bool 대수란?
Bool 대수의 표기법과 그 예
|
|
|
게이트
입력
출력
A
B
Y
0
0
0
0
1
1
1
0
1
1
1
0
(f) Exclusive-OR 게이트
조합논리회로의 설계
우선 원하는 회로의 입력과 출력의 관계를 진리표로 표현을 한다. 그 다음은 구현된 진리표를 가지고 대수식을 세우는 것인데 간력한 경우에는
|
|
|
논리회로 실험(TTL 게이트와 PLD를 이용한), 에드텍
김상진(1990), 디지탈 IC의 활용(게이트에서 마이컴까지), 집문당
문경주(2010), 분산전원 운용을 위한 통신 게이트웨이 개발, 명지대학교
이옥란(2008), 논리 및 부울대수에 관한 연구, 인제대학교
|
|
|
논리식을 간소화
■ 구성형태
▢ 변수가 개수가 n일 경우 2n 개의 사각형들로 구성
▢ 각각의 사각형들은 하나의 최소항을 나타냄 ▣ 부울대수(Boolean Algebra)
▣ 논리게이트(Logic Gate)
▣ 카르노맵(Karnaugh Map)
▇ 2변수, 3변
|
|
|
부울대수(boolean algebra)의 개념
Basic Laws
OR 연산
AND 연산
2중 보수(Double Inversion)와 드모르강(De Morgan)의 법칙
쌍대성 정리 (Duality Theorem)
Fundamental Products
부울함수의 대수적 간소화
consensus의 정리
정규형
진리표로부터 부울
|
|
|
게이트의 조합논리이다.
④ XNOR은 XOR의 보수를 구할 수 있다.
(∵ 왜냐하면 카르노 맵으로 표현 가능한 모든 논리회로는 NOR이나 NAND 만으로 표현 가능하기 때문이다. ) 부울대수의 정리
예비 보고서
1. 실험 목적
2. 기본 이론
3.
|
|
|
논리회로를 구성한다.
예비 문제
1. 다음 논리식을 부울 정리 및 공리를 이용하여 증명하시오.
⑴ A+AB=A
☞ 부울정리 7
⑵ A+B=A+B
☞ 부울정리 8
⑶ (A+B)(A+C)=A+BC
☞ 부울정리 3 분배법칙
2. 부울대수를 사용하여 다음 식을 최대한 간소화하시오.
⑴
|
|
|
게이트 레벨 논리 검증 시스템, 대한전자공학회, 1987 Ⅰ. 논리게이트의 개요
1. 기본적인 논리게이트
2. 응용한 게이트
1) 논리곱(AND)
2) 논리합(OR)
3) 논리부정(NOT)
4) 배타적 논리합(EXCLUCIVE OR)
3. 부울 대수
1) 불 대수 공리
2) 불 대수 기
|
|
메뉴펼치기
