|
Step 입력에 대한 2차 시스템 응답 특성
2. Problem 풀이
3. Root-Locus 와 Nyquist Diagram에서 Gain영향
4. 실험 시스템 전달함수와 pole, zero, steady error
3. 실험결과
1. Root Locus와 게인 값 K의 변화에 따른 시스템의 특성 변화
4. 토의 및 고찰
|
|
|
있도록 Programming 되어있다. 이 Program은 기존에 제시한 전달함수 계산(systf.m)을 참고한다.
Program Source는 다음과 같다.
1) 일 때
가. Root-locus
나. 시간영역 응답곡선 및 주파수 응답곡선
2) 일 때
가. Root-locus
나. 시간영역 응답곡선 및 주파수 응답곡
|
|
|
root locus을 Matlab을 이용하여 나타내 보겠다.
이제 부턴 우리가 원하는 값에 맞게 PID 제어기를 설계해 보겠다. 먼저, PD 제어기 설계부터 시작해 보겠다. 시스템의 overshoot을 43%로 유지하면서, settling time을 2배로 줄일 수 있는 제어기를 설계해 보
|
|
|
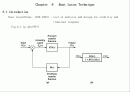
8.1 Introduction
Root locus(Evans, 1948:1950) : tool of analysis and design for stability and transient response
Fig.8.1 (p.424)에서
*K의 변화에 의한 pole의 변화궤적을 root locus라고 한다 8.1 Introduction
8.2 Defining the Root Locus
8.3 Properties of the Root Locus
8.4 Sketching th
|
|
|
Root locus를 그려보면 다음과 같다.
값과 Root locus값이 일치하는 근을 찾아내면 이론값으로 K값은 3.9365이다. 극점 값은 -1±1.736j 이다. 이때의 최고시간(Tp)값은 다음과 같이 구한다.
정착시간(Ts)는 다음과 같다.
입력이 Step 입력일 경우, 정상상태
|
|
메뉴펼치기
