목차
1. 순서쌍과 좌표
2. 함수의 그래프
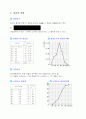
1. 자료의 정리
1. 도수분포표
2. 자료의 관찰
3. 기본도형
1. 직선과 선분
4. 위치관계
5. 작도와 도형의 합동
6. 다각형과 원
7. 다면체와 회전체
9. 입체도형
2. 함수의 그래프
1. 자료의 정리
1. 도수분포표
2. 자료의 관찰
3. 기본도형
1. 직선과 선분
4. 위치관계
5. 작도와 도형의 합동
6. 다각형과 원
7. 다면체와 회전체
9. 입체도형
본문내용
그 끼인각의 크기가 같다.
3.대응하는 한변의 길이가 같고, 그 양끝각의 크기가 각각 같다.
6. 다각형과 원
삼각형
한 직선 위에 있지 않은 세 점 A, B, C 와 선분 AB, 선분 BC, 선분 CA로 이루어진 도형을 삼각형 ABC (또는 △ABC )라고 한다.
▶삼각형의 두 변의 길이의 합은 나머지 한 변의 길이보다 크다.
삼각형의 내각과 외각
▶삼각형의 세 내각의 크기의 합은 180°이다.
▶삼각형의 외각의 크기의 합은 360°이다.
▶삼각형의 한 외각의 크기는 그와 이웃하지 않는 두 내각의 크기의 합과 같다.
다각형
3개 이상의 선분으로 둘러싸인 도형을 다각형 이라고 한다.
n각형의 대각선의 개수
▶한 꼭지점에서 그을 수 있는 대각선의 개수 : (n-3) 개
▶대각선의 총수 :
다각형의 내각과 외각의 크기의 합
▶(n각형의 내각의 크기의 합) = 180°×(n-2)
▶(n각형의 외각의 크기의 합) = 360°
정다각형
모든 변의 길이가 같고 모든 내각의 크기가 같은 다각형
▶(정n각형의 한 내각의 크기) =
▶(정n각형의 한 외각의 크기) =
원과 부채꼴
* 중심각의 크기와 호의 길이
한 원 또는 합동인 두 원에서
▶같은 크기의 중심각에 대한 호의 길이는 같다.
▶호의 길이는 중심각의 크기에 정비례한다.
* 중심각과 현의 길이
한 원 또는 합동인 두 원에서
▶같은 크기의 중심각에 대한 현의 길이는 같다.
▶현의 길이는 중심각의 크기에 정비례하지 않는다.
* 호의 길이와 부채꼴의 넓이
- 호의 길이 : l = 2πr ×(x / 360 )
- 부채꼴의 넓이 : s =πr2 ×( x / 360 )
원과 직선 위치관계
원과 접선
1. 접선의 성질
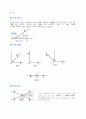
원의 접선은 그 접점과 원의 중심을 연결하는 선분(반지름)에 수직이다.
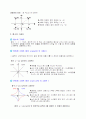
2. 접선의 길이
원의 외부의 한 점에서 원에 그은 두 접선의 길이는 같다.
▶
▶ △POT ≡ △POT`
▶ ∠TPT` + ∠TOT` = 180°
7. 다면체와 회전체
1. 다면체
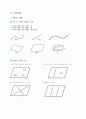
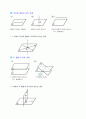
다면체
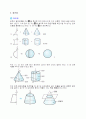
위의 입체도형은 각각 4, 5, 6개의 다각형으로 된 면으로 둘러싸여 있다. 이와 같이 몇 개의 다각형으로 둘러싸인 입체도형을 다면체 라고 한다. 다면체는 그 면의 개수에 따라 사면체, 오면체, 육면체, …로 나뉜다.
각기둥
위의 그림과 같이 두 밑면이 합동인 다각형으로 평행하고 옆면이 모두 직사각형인 다면체를 각기둥 이라고 한다. 밑면인 다각형의 변의 개수에 따라 삼각기둥, 사각기둥, …이라고 한다.
각뿔
밑면이 다각형이고 옆면이 모두 삼각형인 다면체를 각뿔이라고 한다. 각뿔은 밑면인 다각형의 변의 개수에 따라 삼각뿔, 사각뿔, 오각뿔, …로 나뉜다. 각뿔대
각뿔을 밑면에 평행인 평면으로 자를 때 생기는 두 입체도형 중에서, 각뿔이 아닌 쪽의 다면체를 각뿔대 라고 한다. 각뿔대는 밑면인 다각형의 변의 개수에 따라 삼각뿔대, 사각뿔대, 오각뿔대, …로 나누어진다.
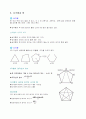
정다면체
정육면체에서 각 꼭지점에 모이는 면의 개수는 모두 3개이며, 각 면은 정사각형으로 되어 있다. 이와 같이 각 면이 모두 합동인 정다각형이고 각 꼭지점에 모이는 면의 개수가 같은 다면체를 정다면체 라고 한다. 정다면체는 다음 그림과 같이 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체의 5가지뿐이다.
2. 회전체
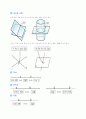
회전체
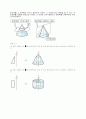
왼쪽의 평면도형을 직선 을 축으로 하여 회전시키면 각각 오른쪽 그림과 같은 입체도형이 생긴다. 이와 같이 한 직선 을 축으로 하여 평면도형을 회전시킬 때 생기는 입체도형을 회전체 라고 한다. 이 때 직선 은 회전축이다. (1) 원뿔(2) 원기둥(3) 구
위의 (1), (2) 에서 선분 AB가 회전하여 생기는 면은 각각의 옆면이 된다. 이 때 선분 AB를 각각의 모선 이라고 한다. 위의 왼쪽 평면도형을 회전했을 때 생기는 입체도형과 같이 원뿔을 밑면에 평행한 평면으로 잘라서 생기는 두 입체도형 중에서 원뿔이 아닌 쪽을 원뿔대 라고 한다.회전체를 그 회전축에 수직인 평면으로 자르면, 그 단면은 항상 원임을 알 수 있다. 또 회전축을 포함한 평면으로 자르면 그 단면은 모두 합동이며 회전축을 대칭축으로 하는 선대칭도형이다.
◀◀ 보기
(1) 왼쪽 도형을 직선 을 회전축으로 하여 한 바퀴 회전시킬 때 생기는 회전체는 오른쪽과 같다. (2) 왼쪽 도형을 직선 을 회전축으로 하여 한 바퀴 회전시킬 때 생기는 회전체는 오른쪽과 같다.
9. 입체도형
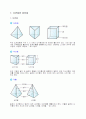
각기둥의 겉넓이와 부피
1) 각기둥의 겉넓이는 다음과 같이 구한다. 2) 각기둥의 부피는 다음과 같이 구한다.
(각기둥의 겉넓이)=(옆넓이)+(밑넓이)×2 (각기둥의 부피)=(밑넓이)×(높이)
원기둥의 겉넓이와 부피
1) 원기둥의 겉넓이는 다음과 같이 구한다. 2) 원기둥의 부피는 다음과 같이 구한다.
(원기둥의 겉넓이)=(옆넓이)+(밑넓이)×2 (원기둥의 부피)=(밑넓이)×(높이)
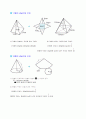
각뿔의 겉넓이와 부피
1)각뿔의 겉넓이는 다음과 같이 구한다 2) 각뿔의 부피는 다음과 같이 구한다.
(각뿔의 겉넓이)=(밑넓이)+(옆넓이) (각뿔의 부피) = (밑넓이)×(높이)×
(각뿔의 부피는 밑넓이와 높이가 같은 각기둥 부피의 )
원뿔의 겉넓이와 부피
1) 원뿔의 전개도에서 원뿔의 겉넓이 는 다음과 같다. (밑넓이)+(옆넓이) (원의 넓이)+(부채꼴의 넓이)
2) 원뿔의 부피는 다음과 같이 구한다.
(원뿔의 부피) = (밑넓이)×(높이)×
(원뿔의 부피는 밑넓이와 높이가 같은 원기둥의 부피의 이다)
구의 겉넓이
구의 절반인 반구의 겉면에 끈을 감은 후, 여기에 감긴 끈의 배가 되는 길이의 끈으로 평면 위에 원을 만들면 그 원의 반지름은 구의 반지름의 배가 된다. 따라서 반지름의 길이가 인 구의 겉넓이를 라 하면 다음과 같다.
구의 겉넓이와 부피
(구의 부피) (원기둥의 부피) 위의 그림과 같이 반지름의 길이가 인 원을 밑면으로 하고, 높이가 인 원기둥 모양의 그릇이 있다. 이 그릇에 물을 가득 채운 다음 반지름의 길이가 인 구를 넣었다가 꺼내면 남아 있는 물의 깊이는 원기둥의 높이의 이 됨을 알 수 있다. 따라서 구의 부피는 원기둥의 부피의 이므로, 반지름의 길이가 인 구의 부피를 라 하면 다음과 같다.
3.대응하는 한변의 길이가 같고, 그 양끝각의 크기가 각각 같다.
6. 다각형과 원
삼각형
한 직선 위에 있지 않은 세 점 A, B, C 와 선분 AB, 선분 BC, 선분 CA로 이루어진 도형을 삼각형 ABC (또는 △ABC )라고 한다.
▶삼각형의 두 변의 길이의 합은 나머지 한 변의 길이보다 크다.
삼각형의 내각과 외각
▶삼각형의 세 내각의 크기의 합은 180°이다.
▶삼각형의 외각의 크기의 합은 360°이다.
▶삼각형의 한 외각의 크기는 그와 이웃하지 않는 두 내각의 크기의 합과 같다.
다각형
3개 이상의 선분으로 둘러싸인 도형을 다각형 이라고 한다.
n각형의 대각선의 개수
▶한 꼭지점에서 그을 수 있는 대각선의 개수 : (n-3) 개
▶대각선의 총수 :
다각형의 내각과 외각의 크기의 합
▶(n각형의 내각의 크기의 합) = 180°×(n-2)
▶(n각형의 외각의 크기의 합) = 360°
정다각형
모든 변의 길이가 같고 모든 내각의 크기가 같은 다각형
▶(정n각형의 한 내각의 크기) =
▶(정n각형의 한 외각의 크기) =
원과 부채꼴
* 중심각의 크기와 호의 길이
한 원 또는 합동인 두 원에서
▶같은 크기의 중심각에 대한 호의 길이는 같다.
▶호의 길이는 중심각의 크기에 정비례한다.
* 중심각과 현의 길이
한 원 또는 합동인 두 원에서
▶같은 크기의 중심각에 대한 현의 길이는 같다.
▶현의 길이는 중심각의 크기에 정비례하지 않는다.
* 호의 길이와 부채꼴의 넓이
- 호의 길이 : l = 2πr ×(x / 360 )
- 부채꼴의 넓이 : s =πr2 ×( x / 360 )
원과 직선 위치관계
원과 접선
1. 접선의 성질
원의 접선은 그 접점과 원의 중심을 연결하는 선분(반지름)에 수직이다.
2. 접선의 길이
원의 외부의 한 점에서 원에 그은 두 접선의 길이는 같다.
▶
▶ △POT ≡ △POT`
▶ ∠TPT` + ∠TOT` = 180°
7. 다면체와 회전체
1. 다면체
다면체
위의 입체도형은 각각 4, 5, 6개의 다각형으로 된 면으로 둘러싸여 있다. 이와 같이 몇 개의 다각형으로 둘러싸인 입체도형을 다면체 라고 한다. 다면체는 그 면의 개수에 따라 사면체, 오면체, 육면체, …로 나뉜다.
각기둥
위의 그림과 같이 두 밑면이 합동인 다각형으로 평행하고 옆면이 모두 직사각형인 다면체를 각기둥 이라고 한다. 밑면인 다각형의 변의 개수에 따라 삼각기둥, 사각기둥, …이라고 한다.
각뿔
밑면이 다각형이고 옆면이 모두 삼각형인 다면체를 각뿔이라고 한다. 각뿔은 밑면인 다각형의 변의 개수에 따라 삼각뿔, 사각뿔, 오각뿔, …로 나뉜다. 각뿔대
각뿔을 밑면에 평행인 평면으로 자를 때 생기는 두 입체도형 중에서, 각뿔이 아닌 쪽의 다면체를 각뿔대 라고 한다. 각뿔대는 밑면인 다각형의 변의 개수에 따라 삼각뿔대, 사각뿔대, 오각뿔대, …로 나누어진다.
정다면체
정육면체에서 각 꼭지점에 모이는 면의 개수는 모두 3개이며, 각 면은 정사각형으로 되어 있다. 이와 같이 각 면이 모두 합동인 정다각형이고 각 꼭지점에 모이는 면의 개수가 같은 다면체를 정다면체 라고 한다. 정다면체는 다음 그림과 같이 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체의 5가지뿐이다.
2. 회전체
회전체
왼쪽의 평면도형을 직선 을 축으로 하여 회전시키면 각각 오른쪽 그림과 같은 입체도형이 생긴다. 이와 같이 한 직선 을 축으로 하여 평면도형을 회전시킬 때 생기는 입체도형을 회전체 라고 한다. 이 때 직선 은 회전축이다. (1) 원뿔(2) 원기둥(3) 구
위의 (1), (2) 에서 선분 AB가 회전하여 생기는 면은 각각의 옆면이 된다. 이 때 선분 AB를 각각의 모선 이라고 한다. 위의 왼쪽 평면도형을 회전했을 때 생기는 입체도형과 같이 원뿔을 밑면에 평행한 평면으로 잘라서 생기는 두 입체도형 중에서 원뿔이 아닌 쪽을 원뿔대 라고 한다.회전체를 그 회전축에 수직인 평면으로 자르면, 그 단면은 항상 원임을 알 수 있다. 또 회전축을 포함한 평면으로 자르면 그 단면은 모두 합동이며 회전축을 대칭축으로 하는 선대칭도형이다.
◀◀ 보기
(1) 왼쪽 도형을 직선 을 회전축으로 하여 한 바퀴 회전시킬 때 생기는 회전체는 오른쪽과 같다. (2) 왼쪽 도형을 직선 을 회전축으로 하여 한 바퀴 회전시킬 때 생기는 회전체는 오른쪽과 같다.
9. 입체도형
각기둥의 겉넓이와 부피
1) 각기둥의 겉넓이는 다음과 같이 구한다. 2) 각기둥의 부피는 다음과 같이 구한다.
(각기둥의 겉넓이)=(옆넓이)+(밑넓이)×2 (각기둥의 부피)=(밑넓이)×(높이)
원기둥의 겉넓이와 부피
1) 원기둥의 겉넓이는 다음과 같이 구한다. 2) 원기둥의 부피는 다음과 같이 구한다.
(원기둥의 겉넓이)=(옆넓이)+(밑넓이)×2 (원기둥의 부피)=(밑넓이)×(높이)
각뿔의 겉넓이와 부피
1)각뿔의 겉넓이는 다음과 같이 구한다 2) 각뿔의 부피는 다음과 같이 구한다.
(각뿔의 겉넓이)=(밑넓이)+(옆넓이) (각뿔의 부피) = (밑넓이)×(높이)×
(각뿔의 부피는 밑넓이와 높이가 같은 각기둥 부피의 )
원뿔의 겉넓이와 부피
1) 원뿔의 전개도에서 원뿔의 겉넓이 는 다음과 같다. (밑넓이)+(옆넓이) (원의 넓이)+(부채꼴의 넓이)
2) 원뿔의 부피는 다음과 같이 구한다.
(원뿔의 부피) = (밑넓이)×(높이)×
(원뿔의 부피는 밑넓이와 높이가 같은 원기둥의 부피의 이다)
구의 겉넓이
구의 절반인 반구의 겉면에 끈을 감은 후, 여기에 감긴 끈의 배가 되는 길이의 끈으로 평면 위에 원을 만들면 그 원의 반지름은 구의 반지름의 배가 된다. 따라서 반지름의 길이가 인 구의 겉넓이를 라 하면 다음과 같다.
구의 겉넓이와 부피
(구의 부피) (원기둥의 부피) 위의 그림과 같이 반지름의 길이가 인 원을 밑면으로 하고, 높이가 인 원기둥 모양의 그릇이 있다. 이 그릇에 물을 가득 채운 다음 반지름의 길이가 인 구를 넣었다가 꺼내면 남아 있는 물의 깊이는 원기둥의 높이의 이 됨을 알 수 있다. 따라서 구의 부피는 원기둥의 부피의 이므로, 반지름의 길이가 인 구의 부피를 라 하면 다음과 같다.
키워드
추천자료
 [과외]중학 수학 중1-2기말 1입체도형(핵심기출)
[과외]중학 수학 중1-2기말 1입체도형(핵심기출) [과외]중학 수학 중3-1기말 1이차방정식과 그해(단원평가)
[과외]중학 수학 중3-1기말 1이차방정식과 그해(단원평가) [과외]중학 수학 중3-1기말 1이차방정식과 그해(핵심기출1)
[과외]중학 수학 중3-1기말 1이차방정식과 그해(핵심기출1) [과외]중학 수학 중3-1기말 1이차방정식과 그해(핵심기출2)
[과외]중학 수학 중3-1기말 1이차방정식과 그해(핵심기출2) [과외]중학 수학 중3-1기말 2이차함수(핵심기출1)
[과외]중학 수학 중3-1기말 2이차함수(핵심기출1) [과외]중학 수학 중3-1기말 2이차함수(핵심기출2)
[과외]중학 수학 중3-1기말 2이차함수(핵심기출2) [과외]중학 수학 중3-1기말 2이차함수(핵심기출3)
[과외]중학 수학 중3-1기말 2이차함수(핵심기출3) [과외]중학 수학 중3-1기말 2이차함수(핵심기출4)
[과외]중학 수학 중3-1기말 2이차함수(핵심기출4) [과외]중학 수학 중3-1중간 1수와 그 계산(핵심기출1)
[과외]중학 수학 중3-1중간 1수와 그 계산(핵심기출1) [과외]중학 수학 중3-1중간 1수와 그 계산(핵심기출2)
[과외]중학 수학 중3-1중간 1수와 그 계산(핵심기출2) [과외]중학 수학 중3-1중간 1수와 그 계산(핵심기출3)
[과외]중학 수학 중3-1중간 1수와 그 계산(핵심기출3) [과외]중학 수학 중3-1중간 2식의계산(핵심기출1)
[과외]중학 수학 중3-1중간 2식의계산(핵심기출1) [과외]중학 수학 중3-1중간 3이차방정식(핵심기출1)
[과외]중학 수학 중3-1중간 3이차방정식(핵심기출1) 중1) <(과학) 지구과학교재 연구 및 지도법, 수업지도안> Ⅲ. 지각의 물질 1. 광물과 암석 (4)...
중1) <(과학) 지구과학교재 연구 및 지도법, 수업지도안> Ⅲ. 지각의 물질 1. 광물과 암석 (4)...






























소개글